题目内容
(1)已知f(
+1)=x+2
,求f(x);
(2)若二次函数f(x)的图象与x轴交于A(-2,0),B(4,0),且函数的最大值为9,求f(x).
| x |
| x |
(2)若二次函数f(x)的图象与x轴交于A(-2,0),B(4,0),且函数的最大值为9,求f(x).
考点:函数解析式的求解及常用方法,二次函数的性质
专题:函数的性质及应用
分析:(1)令
+1=t,使用换元法求解即可,(2)使用待定系数法,由条件令二次函数两根式f(x)=a(x+2)(x-4),再将函数的最大值为9代入可求的f(x).
| x |
解答:
解:(1)令
+1=t,t≥1,则
=t-1,x=(t-1)2,
则f(
+1)=x+2
即为f(t)=t-1+2(t-1)2=2t2-3t+1,
则f(x)=2x2-3x+1;
(2)由题意设二次函数两根式f(x)=a(x+2)(x-4),
则由图象与x轴交于A(-2,0),B(4,0),有图象对称轴为x=
=1,
此时函数的最大值为9,得f(1)=9,解得a=-1,
则f(x)=-(x+2)(x-4)=-x2+2x+8.
| x |
| x |
则f(
| x |
| x |
则f(x)=2x2-3x+1;
(2)由题意设二次函数两根式f(x)=a(x+2)(x-4),
则由图象与x轴交于A(-2,0),B(4,0),有图象对称轴为x=
| -2+4 |
| 2 |
此时函数的最大值为9,得f(1)=9,解得a=-1,
则f(x)=-(x+2)(x-4)=-x2+2x+8.
点评:本题考查函数解析式的求法使用了待定系数法和换元法,(2)中也可令二次函数f(x)=ax2+bx+c,由条件得f(-2)=0,f(4)=0,f(1)=9,求解.

练习册系列答案
相关题目
两条直线λ1:ax-y=-2,与λ2:2x+6y+c=0相交于点(1,m),且λ1到λ2的角为
π,则a+c+m=( )
| 3 |
| 4 |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-14 |
若一个正三棱柱的三视图及其尺寸如图(单位:cm),则该几何体的体积( ) cm3.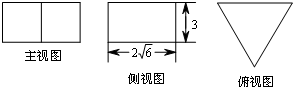

A、12
| ||
B、12
| ||
C、24
| ||
D、24
|
设a,b是异面直线,下列命题正确的是( )
| A、过不在a、b上的一点P一定可以作一条直线和a、b都相交 |
| B、过不在a、b上的一点P一定可以作一个平面和a、b都垂直 |
| C、过a一定可以作一个平面与b垂直 |
| D、过a一定可以作一个平面与b平行 |