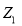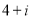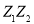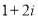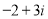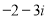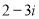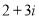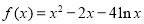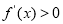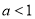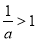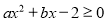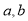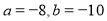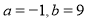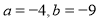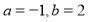题目内容
在数列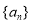 中,
中, .
.
(1)求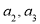 ;
;
(2)设 ,求证:
,求证: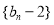 为等比数列;
为等比数列;
(3)求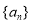 的前
的前 项积
项积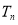 .
.
(1)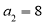 ,
,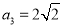 ;(2)证明见试题解析;(3)
;(2)证明见试题解析;(3)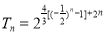 .
.
【解析】
试题分析:(1)根据递推公式直接可求得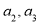 的值;(2)根据条件计算
的值;(2)根据条件计算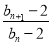 可知其为常数,由此证明结果;(3)首先根据第(2)小题可求得数列数列
可知其为常数,由此证明结果;(3)首先根据第(2)小题可求得数列数列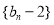 的前
的前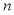 项和,然后利用数列
项和,然后利用数列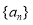 与数列
与数列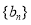 的关系可求得
的关系可求得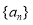 的前
的前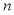 项积
项积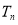 .
.
试题解析:(1)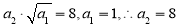 ,
,
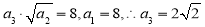 .
.
(2)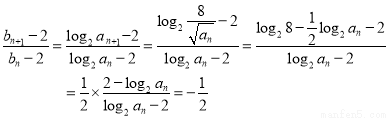 ,
,
∴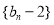 为等比数列,公比为
为等比数列,公比为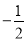 .
.
(3)设数列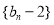 的前
的前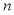 项和为
项和为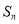
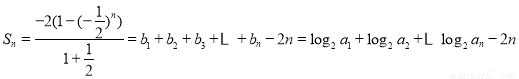
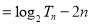
∴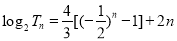 ,∴
,∴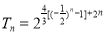 .
.
考点:1.递推数列;2.等比数列的定义、前n项和.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目