题目内容
(14分) 已知函数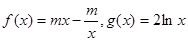 .
.
(1)当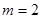 时,求曲线
时,求曲线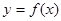 在点
在点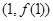 处的切线方程;
处的切线方程;
(2)当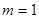 时,判断方程
时,判断方程 实根个数.
实根个数.
(3)若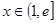 时,不等式
时,不等式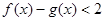 恒成立,求实数
恒成立,求实数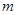 的取值范围.
的取值范围.
【答案】
(1) ;(2)在
;(2)在 内
内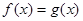 有且仅有一个实数根
有且仅有一个实数根
(3)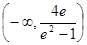
【解析】
试题分析:(1)利用导数的几何意义得到导数的值,切点坐标得到结论。
(2) 时,令
时,令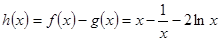 ,
,
求解导数,并判定又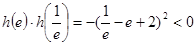 ,
,
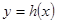 在
在 内有且仅有一个零点进而得到结论。
内有且仅有一个零点进而得到结论。
(3)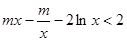 恒成立,
即
恒成立,
即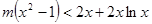 恒成立,
恒成立,
又 ,则当
,则当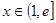 时,
时,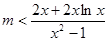 恒成立,
恒成立,
分离参数法构造新函数利用求解的最小值得到参数m的范围。
(1)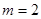 时,
时, ,
,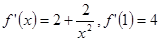 ,切点坐标为
,切点坐标为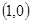 ,
,
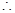 切线方程为
切线方程为
(2) 时,令
时,令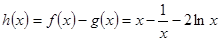 ,
,
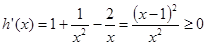 ,
,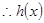 在
在 上为增函数
上为增函数
又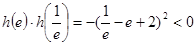 ,
,
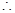
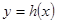 在
在 内有且仅有一个零点
内有且仅有一个零点
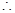 在
在 内
内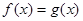 有且仅有一个实数根
有且仅有一个实数根
(或说明 也可以)
也可以)
(3)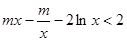 恒成立,
即
恒成立,
即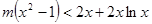 恒成立,
恒成立,
又 ,则当
,则当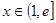 时,
时,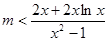 恒成立,
恒成立,
令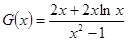 ,只需
,只需 小于
小于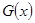 的最小值,
的最小值,
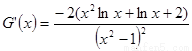 ,
,
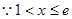 ,
, ,
,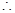 当
当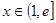 时
时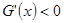 ,
,
 在
在 上单调递减,
上单调递减, 在
在 的最小值为
的最小值为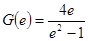 ,
,
则 的取值范围是
的取值范围是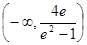
考点:本题主要是考查导数在研究函数中的运用,求解最值和导数几何意义的综合运用。
点评:解决该试题的关键是能将不等式的恒成立问题转化为哈双女户的最值来处理,并得到参数的范围,同时要理解导数的几何意义表示的为切线的斜率。

练习册系列答案
相关题目
 (
( 为自然对数的底数).
为自然对数的底数). 的最小值;
的最小值; ,证明:
,证明: .
. ,其中
,其中 为自然对数的底数.
为自然对数的底数. 时,求曲线
时,求曲线 在
在 处的切线与坐标轴围成的面积;
处的切线与坐标轴围成的面积; 存在一个极大值点和一个极小值点,且极大值与极小值的积为
存在一个极大值点和一个极小值点,且极大值与极小值的积为 ,求
,求 的值.
的值. 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为 ;②
;② 时,
时, ,其中
,其中 .
. 上的解析式,并求出函数
上的解析式,并求出函数 ,
, 时,函数
时,函数 ,若
,若 的图象恒在直线
的图象恒在直线 上方,求实数
上方,求实数 的取值范围(其中
的取值范围(其中 为自然对数的底数,
为自然对数的底数, ).
). .
. 为
为 的极值点,求实数
的极值点,求实数 的值;
的值; 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的取值范围.
的取值范围. (
( ,实数
,实数 ,
, 为常数).
为常数). ,求函数
,求函数 的极值;
的极值; ,讨论函数
,讨论函数