题目内容
在△PAB中,已知A(-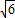 ,0)、B(
,0)、B(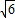 ,0),动点P满足|PA|=|PB|+4.
,0),动点P满足|PA|=|PB|+4.(1)求动点P的轨迹方程;
(2)设M(-2,0),N(2,0),过点N作直线l垂直于AB,且l与直线MP交于点Q,试在x轴上确定一点T,使得PN⊥QT.
【答案】分析:(1)由题意可知动点P的轨迹是以A、B为焦点的双曲线的右支除去其与x轴的交点,且求出双曲线的实半轴和半焦距,利用b2=c2-a2求出b2后可得动点P的轨迹方程;
(2)分别写出直线l与直线MP的方程,求出Q点的坐标(用含有k的代数式表示),设出P点的坐标,把直线MP的方程和双曲线方程联立后利用根与系数的关系求出P点的坐标,再设出T的坐标,写出向量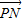
与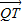 的坐标,由
的坐标,由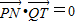 列式可求T的坐标.
列式可求T的坐标.
解答:解:(1)∵|PA|-|PB|=4<|AB|,∴动点P的轨迹是以A、B为焦点的双曲线的右支除去其与x轴的交点.
设双曲线方程为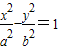 .
.
由已知,得 ,解得
,解得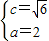 ,∴b2=c2-a2=2.
,∴b2=c2-a2=2.
∴动点P的轨迹方程为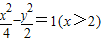 .
.
(2)由题意,直线MP的斜率存在且不为0,设直线l的方程为x=2.
设MP的方程为y=k(x+2).
∵点Q是l与直线MP的交点,∴Q(2,4k).设P(x,y)
由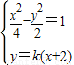 ,整理得(1-2k2)x2-8k2x-(8k2+4)=0
,整理得(1-2k2)x2-8k2x-(8k2+4)=0
则此方程必有两个不等实根x1=-2,x2=x>2.
∴1-2k2≠0,且-2x=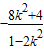 .
.
∴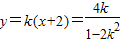 .∴
.∴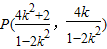 .
.
设T(t,0),要使PN⊥QT,只需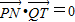 .
.
由N(2,0),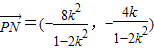 ,
,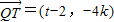 .
.
∴ .
.
∵k≠0,∴t=4,此时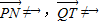 ,∴所求T的坐标为(4,0).
,∴所求T的坐标为(4,0).
点评:本题考查了圆锥曲线的轨迹的求法,考查了直线和圆锥曲线的关系,考查了数学转化思想方法.直线与曲线联立,利用方程的根与系数的关系解题是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是难题.
(2)分别写出直线l与直线MP的方程,求出Q点的坐标(用含有k的代数式表示),设出P点的坐标,把直线MP的方程和双曲线方程联立后利用根与系数的关系求出P点的坐标,再设出T的坐标,写出向量
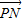
与
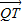 的坐标,由
的坐标,由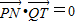 列式可求T的坐标.
列式可求T的坐标.解答:解:(1)∵|PA|-|PB|=4<|AB|,∴动点P的轨迹是以A、B为焦点的双曲线的右支除去其与x轴的交点.
设双曲线方程为
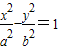 .
.由已知,得
 ,解得
,解得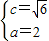 ,∴b2=c2-a2=2.
,∴b2=c2-a2=2.∴动点P的轨迹方程为
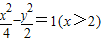 .
.(2)由题意,直线MP的斜率存在且不为0,设直线l的方程为x=2.
设MP的方程为y=k(x+2).
∵点Q是l与直线MP的交点,∴Q(2,4k).设P(x,y)
由
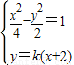 ,整理得(1-2k2)x2-8k2x-(8k2+4)=0
,整理得(1-2k2)x2-8k2x-(8k2+4)=0则此方程必有两个不等实根x1=-2,x2=x>2.
∴1-2k2≠0,且-2x=
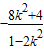 .
.∴
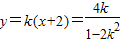 .∴
.∴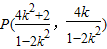 .
.设T(t,0),要使PN⊥QT,只需
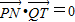 .
.由N(2,0),
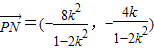 ,
,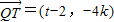 .
.∴
 .
.∵k≠0,∴t=4,此时
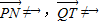 ,∴所求T的坐标为(4,0).
,∴所求T的坐标为(4,0).点评:本题考查了圆锥曲线的轨迹的求法,考查了直线和圆锥曲线的关系,考查了数学转化思想方法.直线与曲线联立,利用方程的根与系数的关系解题是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是难题.

练习册系列答案
相关题目