题目内容
(本小题12分)
已知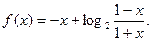
(1)求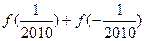 的值;
的值;
(2)当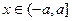 (其中
(其中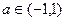 ,且a为常数)时,f(x)是否存在最小值,如果存在,求出最小值;如果不存在,请说明理由。
,且a为常数)时,f(x)是否存在最小值,如果存在,求出最小值;如果不存在,请说明理由。
已知
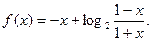
(1)求
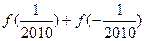 的值;
的值;(2)当
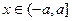 (其中
(其中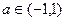 ,且a为常数)时,f(x)是否存在最小值,如果存在,求出最小值;如果不存在,请说明理由。
,且a为常数)时,f(x)是否存在最小值,如果存在,求出最小值;如果不存在,请说明理由。(1)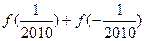 =0
=0
(2)当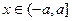 时,f(x)有最小值,且最小值为
时,f(x)有最小值,且最小值为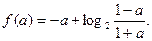
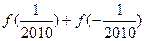 =0
=0(2)当
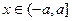 时,f(x)有最小值,且最小值为
时,f(x)有最小值,且最小值为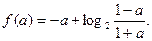
解:(1)由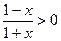 得:
得: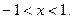 所以f(x)的定义域为:(-1,1),
所以f(x)的定义域为:(-1,1),
又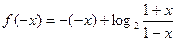
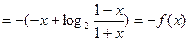 ,
,
所以f(x)为奇函数,所以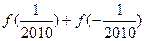 =0.
=0.
(2)f(x)在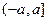 上有最小值,设
上有最小值,设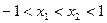 ,
,
则 ,因为
,因为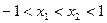 ,所以
,所以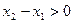 ,
,
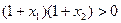 ,所以
,所以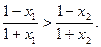
所以函数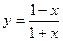 在(-1,1)上是减函数。
在(-1,1)上是减函数。
从而得: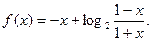 在(-1,1)上也是减函数,又
在(-1,1)上也是减函数,又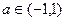 ,
,
所以当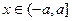 时,f(x)有最小值,且最小值为
时,f(x)有最小值,且最小值为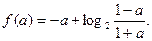
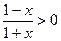 得:
得: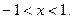 所以f(x)的定义域为:(-1,1),
所以f(x)的定义域为:(-1,1),又
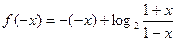
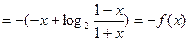 ,
,所以f(x)为奇函数,所以
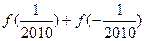 =0.
=0.(2)f(x)在
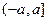 上有最小值,设
上有最小值,设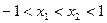 ,
,则
 ,因为
,因为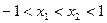 ,所以
,所以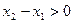 ,
,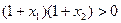 ,所以
,所以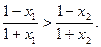
所以函数
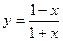 在(-1,1)上是减函数。
在(-1,1)上是减函数。从而得:
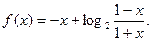 在(-1,1)上也是减函数,又
在(-1,1)上也是减函数,又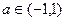 ,
,所以当
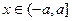 时,f(x)有最小值,且最小值为
时,f(x)有最小值,且最小值为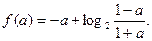

练习册系列答案
相关题目
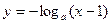 (0<a<1)的图象大致是
(0<a<1)的图象大致是

 x
x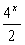
 +1
+1 的图象经过点A,若点A在直线
的图象经过点A,若点A在直线 上,其中
上,其中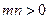 ,则
,则 的最小值为
的最小值为 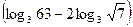 ·
·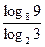 的值是( )
的值是( )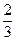
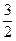
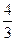
 ,且
,且 ,则
,则 的取值范围是
的取值范围是



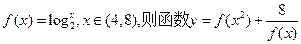 的值域为( )
的值域为( )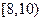
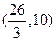
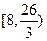
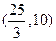
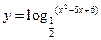 的单调递增区间为 。
的单调递增区间为 。