题目内容
关于优选法有如下一些说法:①若目标函数为单峰函数,则最佳点与好点在差点的同侧;②黄金分割法是最常用的单因素单峰目标函数的优选法之一;③用0.618法确定试点时,n次试验后的精度为δn=0.618n;④分数法一旦用
确定了第一个试点,后续试点可以用“加两头,减中间”的方法来确定.这些说法中正确的序号是
| Fn-1 | Fn |
①②④
①②④
.分析:根据优选法及分数法、黄金分割法-0.618法的优选法则,我们对四个选项一一加以判断即可得出答案.
解答:解:对于①.“若目标函数为单峰函数,则最佳点与好点”,这是缩小试验范围时,保留好点所在部分的重要理论根据.故正确;
对于②,黄金分割法是最常用的单因素单峰目标函数的优选法之一;正确.
对于③,用0.618法确定试点时,n次试验后的精度为δn=0.618n-1;故③错.
对于④,分数法一旦用
确定了第一个试点,后续试点可以用“加两头,减中间”的方法来确定.正确.
故答案为:①②④.
对于②,黄金分割法是最常用的单因素单峰目标函数的优选法之一;正确.
对于③,用0.618法确定试点时,n次试验后的精度为δn=0.618n-1;故③错.
对于④,分数法一旦用
| Fn-1 |
| Fn |
故答案为:①②④.
点评:本题考查的知识点是优选法中的分数法:一般地,用分数法安排试点时,可以分两种情况考虑.(1)可能的试点总数正好是某一个(Fn-1).(2)所有可能的试点总数大于某一(Fn-1),而小于(Fn+1-1).这时可以用分数法解决.分数法的适用范围:目标函数为单峰函数,可以应用于试点只能取整数值或某些特定数的情形,以及限定次数或给定精确度的问题,因为和0.618一样,这些分数都是黄金分割常数的近似值,所以对试验范围为连续的情形也可以用.

练习册系列答案
相关题目
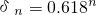 ;④分数法一旦用
;④分数法一旦用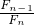 确定了第一个试点,后续试点可以用“加两头,减中间”的方法来确定.这些说法中正确的序号是________.
确定了第一个试点,后续试点可以用“加两头,减中间”的方法来确定.这些说法中正确的序号是________.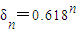 ;④分数法一旦用
;④分数法一旦用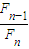 确定了第一个试点,后续试点可以用“加两头,减中间”的方法来确定.这些说法中正确的序号是 .
确定了第一个试点,后续试点可以用“加两头,减中间”的方法来确定.这些说法中正确的序号是 .