题目内容
已知x、y满足以下约束条件
，则z=x2+y2的最大值和最小值分别是（ ）
|
分析：已知x、y满足以下约束条件
，画出可行域，目标函数z=x2+y2是可行域中的点（x，y）到原点的距离的平方，利用线性规划进行求解；
|
解答：
解：如图，作出可行域，x2+y2是点（x，y）到原点的距离的平方，
故最大值为点A（2，3）到原点的距离的平方，
即|AO|2=13，
最小值为原点到直线2x+y-2=0的距离的平方，
即为
，
故选C．
解：如图，作出可行域，x2+y2是点（x，y）到原点的距离的平方，故最大值为点A（2，3）到原点的距离的平方，
即|AO|2=13，
最小值为原点到直线2x+y-2=0的距离的平方，
即为
| 4 |
| 5 |
故选C．
点评：此题主要考查简单的线性规划问题，是一道基础题，要学会画图，考查的知识点比较单一；
练习册系列答案
相关题目
，则z=x2+y2的最大值和最小值分别是（ ）
，
，使z=x+ay（a＞0）取得最小值的最优解有无数个，则a的值为（ ）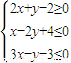
，则z=x2+y2的最大值和最小值分别是（ ）
，