题目内容
设x取实数,则f(x)与g(x)表示同一个函数的是( )
A、f(x)=x,g(x)=
| ||||||||
B、f(x)=
| ||||||||
| C、f(x)=1,g(x)=(x-1)0 | ||||||||
D、f(x)=
|
分析:根据确定函数的三要素判断每组函数是否为同一个函数,即需要确定每组函数的定义域、对应关系、值域是否相同,也可只判断前两项是否相同即可确定这两个函数是否为同一个函数.
解答:解:A组中两函数的定义域相同,对应关系不同,g(x)=|x|≠x,故A中的两函数不为同一个函数;
B组中两函数的定义域均为所有正数构成的集合,对应关系化简为f(x)=g(x)=1,故B中的两函数是同一个函数;
C组中两函数的定义域不同,f(x)的定义域为R,g(x)的定义域由非零实数构成,故C中的两函数不为同一个函数;
D组中两函数的定义域不同,g(x)的定义域为R,f(x)的定义域由不等于-3的实数构成,故D中的两函数不为同一个函数.
故选B.
B组中两函数的定义域均为所有正数构成的集合,对应关系化简为f(x)=g(x)=1,故B中的两函数是同一个函数;
C组中两函数的定义域不同,f(x)的定义域为R,g(x)的定义域由非零实数构成,故C中的两函数不为同一个函数;
D组中两函数的定义域不同,g(x)的定义域为R,f(x)的定义域由不等于-3的实数构成,故D中的两函数不为同一个函数.
故选B.
点评:本题考查函数定义域的求解,函数解析式的化简,考查学生对函数三要素的认识和把握程度,考查学生的转化与化归思想,属于基本的函数题型.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
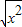
 ,g(x)=
,g(x)=
 ,g(x)=x-3
,g(x)=x-3
 ,g(x)=
,g(x)=
 ,g(x)=x-3
,g(x)=x-3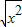
 ,g(x)=
,g(x)=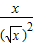
 ,g(x)=x-3
,g(x)=x-3