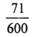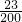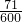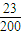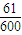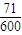题目内容
形如34021这样的数称为“波浪数”,即十位上的数字、千位上的数字均比与它们各自相邻的数字大,现从由0,1,2,3,4,5组成的数字不重复的五位数中任取一个,则该数是“波浪数”的概率为( )A.
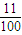
B.
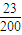
C.
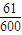
D.
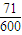
【答案】分析:采用分类计数的办法求解本题,具体分类即要考虑定义“五位波浪数”,也要考虑十位数字、千位数字均比它们各自相邻的数字大,也要考虑特殊数字0在不在首位,具体分法请看解题过程.
解答:解:有0参与时,0不能放在万位数,最大的两个放在一起,分别放在千位和十位,故有 (
( +1+
+1+ •
• •
• )=55种.
)=55种.
没有0时,最大两个数字放在一起,或分别放在千位和十位位置,有 (2
(2 +
+ •
• )=16种,
)=16种,
故“波浪数”共有55+16=71个.
而所有的五位数 有5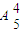 =600个,
=600个,
故该数是“波浪数”的概率为 ,
,
故答案为 .
.
点评:本题考查排列组合及简单计数问题,解决问题的关键是要求出指定的事件由0,1,2,3,4,5可构成不重复的“五位波浪数”的个数,则要对该问题准确分类,做到不重复,不遗漏,正确求解结果.本题极易因为分类不清出错.
解答:解:有0参与时,0不能放在万位数,最大的两个放在一起,分别放在千位和十位,故有
 (
( +1+
+1+ •
• •
• )=55种.
)=55种.没有0时,最大两个数字放在一起,或分别放在千位和十位位置,有
 (2
(2 +
+ •
• )=16种,
)=16种,故“波浪数”共有55+16=71个.
而所有的五位数 有5
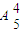 =600个,
=600个,故该数是“波浪数”的概率为
 ,
,故答案为
 .
.点评:本题考查排列组合及简单计数问题,解决问题的关键是要求出指定的事件由0,1,2,3,4,5可构成不重复的“五位波浪数”的个数,则要对该问题准确分类,做到不重复,不遗漏,正确求解结果.本题极易因为分类不清出错.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
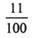 (B)
(B)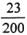 (C)
(C) (D)
(D)