题目内容
17.函数$y=\frac{1}{2-x}$的图象与函数y=2sin(πx-π)(-2≤x≤6)的图象所有交点的横坐标之和等于( )| A. | 4 | B. | 8 | C. | 10 | D. | 16 |
分析 分别作出两个函数的图象,根据图象的对称性即可得到交点坐标问题.
解答 解:作出函数y=$\frac{1}{2-x}$的图象,则函数关于点(2,0)对称,
y=2sin(πx-π)=-2sin(πx),(-2≤x≤6)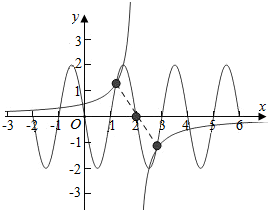
同时点(2,0)也是函数y=-sin(πx),(-2≤x≤6)的对称点,
由图象可知,两个函数在[-2,6]上共有8个交点,两两关于点(2,0)对称,
设对称的两个点的横坐标分别为x1,x2,
则x1+x2=2×2=4,
∴8个交点的横坐标之和为4×4=16.
故选:D
点评 本题主要考查函数交点个数以及数值的计算,根据函数图象的性质,利用数形结合是解决此类问题的关键,综合性较强.

练习册系列答案
相关题目
7. 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则过点P(ω,φ),且斜率为A的直线方程是( )
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则过点P(ω,φ),且斜率为A的直线方程是( )
 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则过点P(ω,φ),且斜率为A的直线方程是( )
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则过点P(ω,φ),且斜率为A的直线方程是( )| A. | y-$\frac{π}{3}$=$\sqrt{3}$(x-2) | B. | y-$\frac{2π}{3}$=$\sqrt{3}$(x-4) | C. | y-$\frac{2π}{3}$=2(x-4) | D. | y-$\frac{2π}{3}$=2(x-2) |
5.已知集合A={y|y=x2},B={x|y=lg(2-x),则A∩B=( )
| A. | A、[0,2] | B. | [0,2) | C. | (-∞,2] | D. | (-∞,2) |
6.函数y=ln(2-x-x2)的单调递减区间为( )
| A. | (-∞,-$\frac{1}{2}$] | B. | (-2,-$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,+∞) | D. | (-$\frac{1}{2}$,1) |
 如图,在平面直角坐标系xoy中,椭圆C的标准方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,直线l与x轴交于点E,与椭圆C交于A,B两点.
如图,在平面直角坐标系xoy中,椭圆C的标准方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,直线l与x轴交于点E,与椭圆C交于A,B两点.