题目内容
设递增等差数列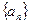 的前
的前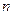 项和为
项和为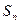 ,已知
,已知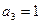 ,
,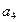 是
是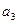 和
和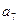 的等比中项,
的等比中项,
(I)求数列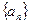 的通项公式
的通项公式
(II )求数列
)求数列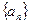 的前
的前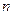 项和
项和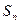
解:在递增等差数列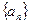 中,设公差为
中,设公差为 ,
,


解得  7分
7分

 所求
所求 ,
, 12分
12分
解析

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
题目内容
设递增等差数列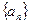 的前
的前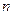 项和为
项和为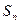 ,已知
,已知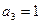 ,
,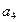 是
是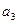 和
和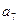 的等比中项,
的等比中项,
(I)求数列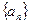 的通项公式
的通项公式
(II )求数列
)求数列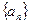 的前
的前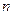 项和
项和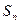
解:在递增等差数列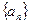 中,设公差为
中,设公差为 ,
,


解得  7分
7分

 所求
所求 ,
, 12分
12分
解析

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案