题目内容
已知点(0,1)和(3,0)都在函数f(x)=
(0≤x≤1)的反函数的图象上.
(1)求b,c的值;
(2)求f(x)的反函数f-1(x).
| c+bx-x2 |
(1)求b,c的值;
(2)求f(x)的反函数f-1(x).
分析:(1)由已知中中点(0,1)和(3,0)都在函数f(x)=
(0≤x≤1)的反函数的图象上,可得(1,0),(0,3)都在函数f(x)=
(1≥x≥0)的图象上,代入构造关于b,c的方程组,进而得到b,c的值;
(2)由(1)中结论,我们可以求出函数f(x)=
(0≤x≤1)的解析式,根据二次函数在闭区间上的最值,我们可以求出函数f(x)的值域(反函数的定义域),反表示后,易求出反函数的解析式,进而得到答案.
| c+bx-x2 |
| c+bx-x2 |
(2)由(1)中结论,我们可以求出函数f(x)=
| c+bx-x2 |
解答:解:(1)由题意知(1,0),(0,3)都在函数f(x)=
(1≥x≥0)的图象上,
得
,
解得
(2)由(1)知f(x)=
(1≥x≥0),
其值域为[0,3]
令y=f(x)=
,
得x=
-4
所以f-1(x)=
-4 (0≤x≤3)
| c+bx-x2 |
得
|
解得
|
(2)由(1)知f(x)=
| 9-8x-x2 |
其值域为[0,3]
令y=f(x)=
| 9-8x-x2 |
得x=
| 25-y2 |
所以f-1(x)=
| 25-x2 |
点评:本题考查的知识点是待定系数法求函数的解析式,反函数,其中(1)的关键是构造关于b,c的方程组,(2)的关键是根据反函数求示的步骤,由原函数解析式求出反函数的解析式,此时易忽略反函数的定义域为原函数的值域,而仅求出反函数的对应关系.

练习册系列答案
相关题目
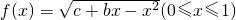 的反函数的图象上.
的反函数的图象上.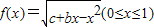 的反函数的图象上.
的反函数的图象上.