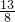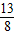题目内容
同时抛掷4枚均匀的硬币3次,设4枚硬币正好出现2枚正面向上,2枚反面向上的次数为ξ,则ξ的数学期望是( )A.

B.

C.
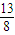
D.1
【答案】分析:先根据随机事件的概率公式求出“在一次抛掷4枚均匀的硬币时,正好出现2枚正面向上,2枚反面向上”的概率.再根据独立重复试验的概率公式,分别求出在三次试验中ξ=i(i=0、1、2、3)的概率,最后根据数学期望的公式,求出随机变量ξ的数学期望.
解答:解:事件“4枚硬币正好出现2枚正面向上,2枚反面向上”的概率为
P=C42•( )4=
)4= ,
,
由此可得P(ξ=0)=C3•(1- )3=(
)3=( )3=
)3=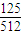 ,
,
P(ξ=1)=C31• .(1-
.(1- )2=
)2=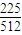 ,
,
P(ξ=2)=C32•( )2.(1-
)2.(1- )=
)=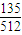 ,
,
P(ξ=3)=C33•( )3=
)3=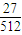 ,
,
由此可得Eξ=0×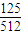 +1×
+1×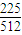 +2×
+2×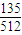 +3×
+3×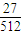 =
= .
.
故选B.
点评:本题以n次独立重复试验为载体,考查了离散型随机变量的期望与方差的知识点,属于基础题.
解答:解:事件“4枚硬币正好出现2枚正面向上,2枚反面向上”的概率为
P=C42•(
 )4=
)4= ,
,由此可得P(ξ=0)=C3•(1-
 )3=(
)3=( )3=
)3=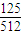 ,
,P(ξ=1)=C31•
 .(1-
.(1- )2=
)2=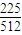 ,
,P(ξ=2)=C32•(
 )2.(1-
)2.(1- )=
)=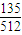 ,
,P(ξ=3)=C33•(
 )3=
)3=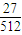 ,
,由此可得Eξ=0×
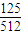 +1×
+1×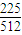 +2×
+2×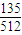 +3×
+3×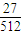 =
= .
.故选B.
点评:本题以n次独立重复试验为载体,考查了离散型随机变量的期望与方差的知识点,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目