Question

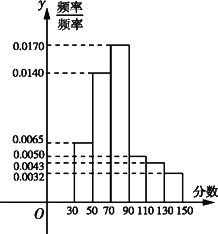
某市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰．若现有500人参加测试，学生成绩的频率分布直方图如下：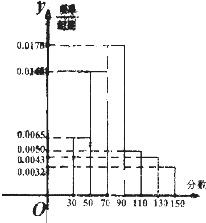
（I）求获得参赛资格的人数；
（II）根据频率直方图，估算这500名学生测试的平均成绩．

Answer 1

分析：（1）求出满足参赛资格的区域包含的长方形的纵坐标的和乘以组距得到分布在该区域的频率，再乘以样本容量求出获得参赛资格的人数．
（2）由频率分布直方图求数据的平均数，是各个矩形宽的中点横坐标乘以各个矩形的纵坐标的和，在乘以组距即可．

解答：解：（1）由频率分布直方图得，获得参赛资格的人数为
500×（0.0050+0.0043+0.0032）×20=125人
（2）设500名学生的平均成绩为

.

x

，则

.

x

=(

30+50

2

×0.0065+

50+70

2

×0.0140+

110+130

2

×0.0043+

130+150

2

×0.032)×20=78.48

点评：在求频率分布直方图中的问题时，特别注意图中的纵坐标是

频率

组距

、利用频率分布直方图求数据的平均数是利用各个矩形的中点横坐标乘以各个矩形的面积和．