Question

某厂使用A，B两种零件装配甲、乙两种产品，该厂每月装配甲产品最多250件，装配乙产品最多120件，已知装配一件甲产品需要4个月A零件，2个B零件，装配一件乙产品需要6个A零件，8个B零件，某月能用的A零件最多为1400个，能用的B林件最多为1200个，已知甲产品每件利润1000元，乙产品每件利润2000元，设该月装配甲、乙产品分别是x、y件，则用不等式组表示x、y满足的条件是

 

（x，y∈N）；该月最大利润为

 

万元．

Answer 1

分析：先设甲、乙两种产品月产量分别为x、y件，写出约束条件、目标函数，欲求生产收入最大值的范围，即求可行域中的最优解，在线性规划的解答题中建议使用直线平移法求出最优解，即将目标函数看成是一条直线，分析目标函数Z与直线截距的关系，进而求出最优解．注意：最后要将所求最优解还原为实际问题．

解答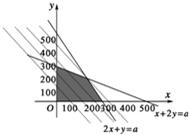：解：设该月装配甲、乙产品分别是x、y件，
约束条件是 

0≤x≤250 0≤y≤120 4x+6y≤1400 2x+8y≤1200

目标函数是z=1000（x+2y）
由约束条件画出可行域，如图
将z=x+2y它变形为y=-

1

2

x+

1

2

z，
这是斜率为-

1

2

、随z变化的一簇直线．

z

2

是直线在y轴上的截距，当

z

2

最大时z最大，当然直线要与可行域相交，即在满足约束条件时目标函数取得最大值．
由

4x+6y=1400 2x+8y=1200

解得 

x=200 y=100

在这个问题中，使z=x+2y取得最大值的（x，y）是两直线4x+6y=1400与2x+8y=120的交点（200，100）
∴z=1×200+2×100=400（千元）
答：每月生产甲180件，生产乙90件月生产收入最大，最大值为40万元．
故答案为：

0≤x≤250 0≤y≤120 4x+6y≤1400 2x+8y≤1200

；40．

点评：在解决线性规划的应用题时，其步骤为：①分析题目中相关量的关系，列出不等式组，即约束条件?②由约束条件画出可行域?③分析目标函数Z与直线截距之间的关系?④使用平移直线法求出最优解?⑤还原到现实问题中．