题目内容
已知抛物线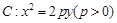 上一点
上一点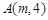 到其焦点的距离为
到其焦点的距离为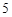 ,则m= .
,则m= .
【答案】
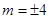
【解析】
试题分析:抛物线的顶点在原点,焦点在y轴上,抛物线上一点(m,4),
∴设抛物线的方程为:x2=2py(p>0),
∴其准线方程为:y= -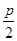 ,
,
∵抛物线上一点P(m,4)到焦点F的距离等于5,
∴由抛物线的定义得:|PF|=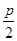 +4=5∴p=2,
+4=5∴p=2,
∴所求抛物线的方程为x2=4y,将x=m代入解析式中,得到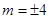 ,故答案为
,故答案为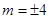 。
。
考点:本题主要是考查抛物线的简单性质,
属于中档题.
点评:解决该试题的关键是考查待定系数法,突出考查抛物线的定义的理解与应用,求得p的值.

练习册系列答案
相关题目
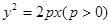 上一点
上一点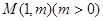 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线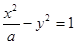 的左顶点为
的左顶点为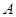 ,若双曲线的一条渐近线与直线
,若双曲线的一条渐近线与直线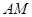 平行,则实数
平行,则实数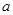 的值是( )
的值是( )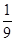 B.
B.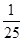 C.
C.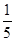 D.
D.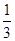
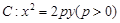 上一点
上一点 到其焦点的距离为
到其焦点的距离为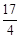 ,则m=
.
,则m=
.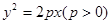 上一点
上一点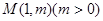 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线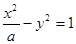 的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数
的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数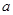 的值是
的值是 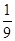 B.
B.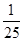 C.
C.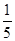 D.
D.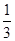
 上一点
上一点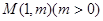 到其焦点的距离为
到其焦点的距离为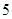 ,双曲线
,双曲线 的左顶点为
的左顶点为 ,若双曲线一条渐近线与直线
,若双曲线一条渐近线与直线 平行,则实数
平行,则实数 等于( )
等于( ) B.
B.
 C.
C.
 D.
D.
