Question

用3种不同颜色给下图的3个矩形随机涂色，每个矩形只涂一种颜色，则3个矩形颜色都不同的概率为

 

．

Answer 1

分析：所有可能的基本事件共有27个，3个矩形颜色都不同共有A₃³=6种情况，根据古典概型概率公式即可求得结果．

解答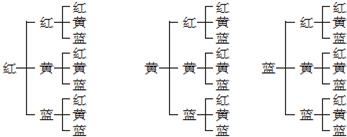：解：所有可能的基本事件共有27个，如图所示．
记“3个矩形颜色都不同”为事件B，由图可知，事件B的基本事件
有2×3=6个，故P（B）=

6

27

=

2

9

．
故答案为：

2

9

点评：本题考查分步计数的原理的运用，注意分析题意，认清是分类问题还是分步问题．属基础题．