题目内容
(本题满分12分)
已知函数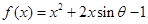 ,
,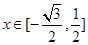
(1)当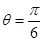 时,求
时,求 的最大值和最小值
的最大值和最小值
(2)若 在
在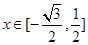 上是单调函数,且
上是单调函数,且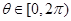 ,求
,求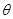 的取值范围
的取值范围
(1) 有最小值
有最小值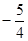 ,有最大值
,有最大值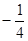 (2)
(2)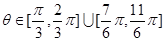
解析试题分析:(1)当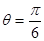 时,
时,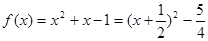
 在
在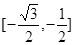 上单调递减,在
上单调递减,在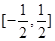 上单调递增
上单调递增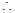 当
当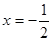 时,函数
时,函数 有最小值
有最小值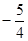
当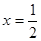 时,函数
时,函数 有最小值
有最小值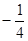 …………………………………(6分)
…………………………………(6分)
(2)要使 在
在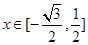 上是单调函数,则
上是单调函数,则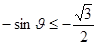 或
或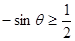
即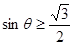 或
或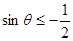 ,又
,又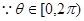
解得: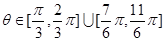 …………………………………(12分)
…………………………………(12分)
考点:二次函数单调性及最值
点评:二次函数求最值结合图像对称轴与定义域,单调区间以对称轴为区间边界

练习册系列答案
相关题目
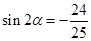 ,
,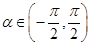 ,求
,求 的值;
的值;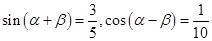 .
.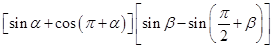 的值.
的值. x+
x+ )(x∈R,
)(x∈R, )的部分图象如图所示。
)的部分图象如图所示。
 )的单调递增区间。
)的单调递增区间。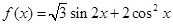 .
. 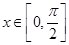 时,求函数f(x)的值域;
时,求函数f(x)的值域;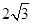 ,求a,b的值。
,求a,b的值。 分别是
分别是 的三个内角
的三个内角 的对边,且满足
的对边,且满足 .
. 的大小;
的大小; 为锐角时,求函数
为锐角时,求函数 的值域.
的值域.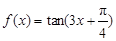
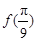 的值;
的值;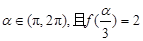 ,求
,求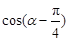 的值.
的值.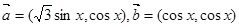 ,
,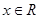 ,函数
,函数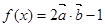 ;
; 的最小正周期;
的最小正周期;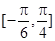 上的最大值和最小值。
上的最大值和最小值。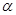 为第三象限角,
为第三象限角,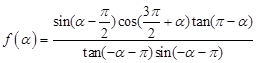 .
.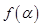 ;
;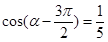 ,求
,求 。
。 的振幅和最小正周期;
的振幅和最小正周期; 时,函数
时,函数 时,求
时,求