题目内容
大学毕业的小张到甲、乙、丙三个单位应聘,各单位是否录用他相互独立,其被录用的概率分别为
、
、
(允许小张被多个单位同时录用).
(1)小张没有被录用的概率;
(2)求小张被2个单位同时录用的概率;
(3)设没有录用小张的单位个数为ξ,求ξ的分布列和它的数学期望.
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
(1)小张没有被录用的概率;
(2)求小张被2个单位同时录用的概率;
(3)设没有录用小张的单位个数为ξ,求ξ的分布列和它的数学期望.
分析:(1)由题意可得:小张被几个学校录取是相互独立的,小张没有被录取即表示小张没有被三个学校中的任何一个录取,进而根据题意得到其概率为:(1-
)(1-
)(1-
)=
.
(2)由题意可得:小张被录取的学校有:甲乙、甲丙、乙丙3种情况,并且这3种情况之间的关系是互斥的,再根据互斥事件的概率公式即可得到答案.
(3)由题意可得:ξ可能取的值为0,1,2,3,再结合题意分别求出其发生的概率,即可得到ξ的分布列,进而求出ξ的数学期望.
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 60 |
(2)由题意可得:小张被录取的学校有:甲乙、甲丙、乙丙3种情况,并且这3种情况之间的关系是互斥的,再根据互斥事件的概率公式即可得到答案.
(3)由题意可得:ξ可能取的值为0,1,2,3,再结合题意分别求出其发生的概率,即可得到ξ的分布列,进而求出ξ的数学期望.
解答:解:(1)∵各单位是否录用小张相互独立,
∴小张被几个学校录取是相互独立的,
∵小张没有被录取即表示小张没有被三个学校中的任何一个录取,并且被录用的概率分别为
、
、
,
∴小张没有被录取的概率是 (1-
)(1-
)(1-
)=
.
(2)由题意可得:小张被2个单位同时录用,即录取的学校有:甲乙、甲丙、乙丙3种情况,
并且这3种情况之间的关系是互斥的,
∴根据互斥事件的概率公式可得:P=
×
×
+
×
×
+
×
×
=
,
所以小张被2个单位同时录用的概率为
.
(3)由题意可得:ξ可能取的值为0,1,2,3,
所以P(ξ=0)=
×
×
=
;P(ξ=1)=
×
×
+
×
×
+
×
×
=
;
P(ξ=2)=
×
×
+
×
×
+
×
×
=
;P(ξ=3)=(1-
)(1-
)(1-
)=
.
所以ξ的分布列为:
所以Eξ=0×
+1×
+2×
+3×
=
.
∴小张被几个学校录取是相互独立的,
∵小张没有被录取即表示小张没有被三个学校中的任何一个录取,并且被录用的概率分别为
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
∴小张没有被录取的概率是 (1-
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 60 |
(2)由题意可得:小张被2个单位同时录用,即录取的学校有:甲乙、甲丙、乙丙3种情况,
并且这3种情况之间的关系是互斥的,
∴根据互斥事件的概率公式可得:P=
| 4 |
| 5 |
| 2 |
| 3 |
| 1 |
| 4 |
| 4 |
| 5 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
| 13 |
| 30 |
所以小张被2个单位同时录用的概率为
| 13 |
| 30 |
(3)由题意可得:ξ可能取的值为0,1,2,3,
所以P(ξ=0)=
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
| 3 |
| 1 |
| 4 |
| 4 |
| 5 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
| 13 |
| 30 |
P(ξ=2)=
| 4 |
| 5 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 5 |
| 2 |
| 3 |
| 1 |
| 4 |
| 3 |
| 20 |
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 60 |
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 2 |
| 5 |
| 13 |
| 30 |
| 3 |
| 20 |
| 1 |
| 60 |
| 47 |
| 60 |
点评:本题主要考查等可能事件发生的概率,解决此类问题的关键是熟练掌握相互独立事件同时发生的概率和互斥事件的概率,本题还考查了离散型随机变量的分布列与期望,此题属于中档题型,高考经常的涉及.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
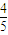 、
、 、
、 (允许小张被多个单位同时录用).
(允许小张被多个单位同时录用).