题目内容
某大学一个专业团队为某专业大学生研究了多款学习软件,其中有A、B、C三种软件投入使用,经一学年使用后,团队调查了这个专业大一四个班的使用情况,从各班抽取的样本人数如下表:
(1)从这12人中随机抽取2人,求这2人恰好来自同一班级的概率;
(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择一款软件,其中选A、B两个软件学习的概率都是
,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为ξ,求ξ的分布列和数学期望.
| 班级 | 一 | 二 | 三 | 四 |
| 人数 | 3 | 2 | 3 | 4 |
(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择一款软件,其中选A、B两个软件学习的概率都是
| 1 |
| 6 |
分析:(1)从12人中抽取2个的所有选法有
,这2人恰好来自同一班级的结果有
+
+
+
,利用古典概率的计算公式可求
(2)由题意可得,每人选择C的概率为1-2×
=
且ξ~B(3,
),从而可求
| C | 2 12 |
| C | 2 3 |
| C | 2 2 |
| C | 2 3 |
| C | 2 4 |
(2)由题意可得,每人选择C的概率为1-2×
| 1 |
| 6 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:(1)从12人中抽取2个的所有选法有
=66种
记:“这2人恰好来自同一班级”为事件A,则A包含的结果有
+
+
+
=13种
∴P(A)=
(2)由题意可得,每人选择C的概率为1-2×
=
则ξ~B(3,
)
∴P(ξ=k)=
(
)k(
)3-k(k=0,1,2,3)
∴Eξ=3×
=2
| C | 2 12 |
记:“这2人恰好来自同一班级”为事件A,则A包含的结果有
| C | 2 3 |
| C | 2 2 |
| C | 2 3 |
| C | 2 4 |
∴P(A)=
| 13 |
| 66 |
(2)由题意可得,每人选择C的概率为1-2×
| 1 |
| 6 |
| 2 |
| 3 |
则ξ~B(3,
| 2 |
| 3 |
∴P(ξ=k)=
| C | k 3 |
| 2 |
| 3 |
| 1 |
| 3 |
∴Eξ=3×
| 2 |
| 3 |
点评:本题主要考查了古典概率的计算公式的应用,解题的关键是利用组合知识准确求出相应问题的结果数,还考查了二项分布的分布列及期望值的求解

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
某大学一个专业团队为某专业大学生研究了多款学习软件,其中有A、B、C三种软件投入使用,经一学年使用后,团队调查了这个专业大一四个班的使用情况,从各班抽取的样本人数如下表
|
班级 |
一 |
二 |
三 |
四 |
|
人数 |
3 |
2 |
3 |
4 |
(1)从这12人中随机抽取2人,求这2人恰好来自同一班级的概率.
(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择A、B两个软件学习的概率每个都是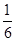 ,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为
,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为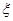 ,求
,求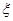 的分布列和数学期望.
的分布列和数学期望.
某大学一个专业团队为某专业大学生研究了多款学习软件,其中有A、B、C三种软件投入使用,经一学年使用后,团队调查了这个专业大一四个班的使用情况,从各班抽取的样本人数如下表:
(1)从这12人中随机抽取2人,求这2人恰好来自同一班级的概率;
(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择一款软件,其中选A、B两个软件学习的概率都是 ,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为ξ,求ξ的分布列和数学期望.
,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为ξ,求ξ的分布列和数学期望.
| 班级 | 一 | 二 | 三 | 四 |
| 人数 | 3 | 2 | 3 | 4 |
(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择一款软件,其中选A、B两个软件学习的概率都是
 ,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为ξ,求ξ的分布列和数学期望.
,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为ξ,求ξ的分布列和数学期望.