题目内容
乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换,每次发球,胜方得1分,负方得0分。设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立。甲、乙的一局比赛中,甲先发球。
(1)求开始第4次发球时,甲、乙的比分为1比2的概率;
(2)ξ表示开始第4次发球时乙的得分,求ξ的期望。
(1)求开始第4次发球时,甲、乙的比分为1比2的概率;
(2)ξ表示开始第4次发球时乙的得分,求ξ的期望。
解:记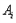 为事件“第i次发球,甲胜”,i=1,2,3,
为事件“第i次发球,甲胜”,i=1,2,3,
则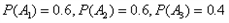 。
。
(1)事件“开始第4次发球时,甲、乙的比分为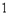 比
比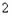 ”为
”为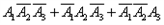 ,
,
由互斥事件有一个发生的概率加法公式得
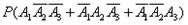

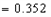 。
。
即开始第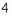 次发球时,甲、乙的比分为
次发球时,甲、乙的比分为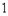 比
比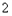 的概率为0.352。
的概率为0.352。
(2)由题意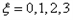 。
。
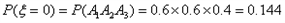 ;
;
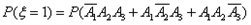
 =0.408;
=0.408;
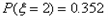 ;
;
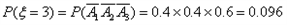
所以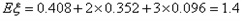 。
。
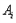 为事件“第i次发球,甲胜”,i=1,2,3,
为事件“第i次发球,甲胜”,i=1,2,3,则
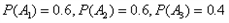 。
。(1)事件“开始第4次发球时,甲、乙的比分为
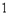 比
比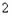 ”为
”为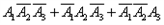 ,
,由互斥事件有一个发生的概率加法公式得
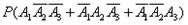

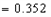 。
。即开始第
 次发球时,甲、乙的比分为
次发球时,甲、乙的比分为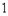 比
比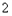 的概率为0.352。
的概率为0.352。(2)由题意
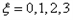 。
。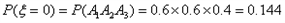 ;
;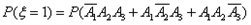
 =0.408;
=0.408;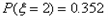 ;
;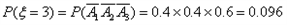
所以
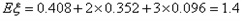 。
。
练习册系列答案
相关题目
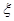 表示开始第4次发球时乙的得分,求
表示开始第4次发球时乙的得分,求