题目内容
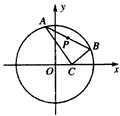
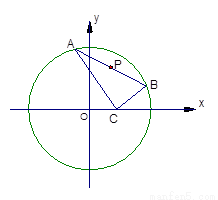
.已知点C(1,0),点A、B是⊙O: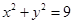 上任意两个不同的点,且满足
上任意两个不同的点,且满足
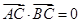 ,设P为弦AB的中点.(1)求点P的轨迹T的方程;(2)试探究在轨迹T上
,设P为弦AB的中点.(1)求点P的轨迹T的方程;(2)试探究在轨迹T上
是否存在这样的点:它到直线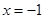 的距离恰好等于到点C的距离?若存在,求出这样的
的距离恰好等于到点C的距离?若存在,求出这样的
点的坐标;若不存在,说明理由.
【答案】
解:(1)连结CP,由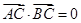 ,知AC⊥BC
,知AC⊥BC
∴|CP|=|AP|=|BP|=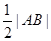 ,由垂径定理知
,由垂径定理知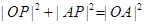
即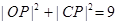 设点P(x,y),有
设点P(x,y),有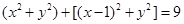
化简,得到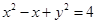
(2)根据抛物线的定义,到直线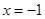 的距离等于到点C(1,0)的距离的点都在抛物线
的距离等于到点C(1,0)的距离的点都在抛物线
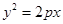 上,其中
上,其中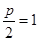 ,∴
,∴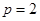 ,故抛物线方程为
,故抛物线方程为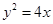
由方程组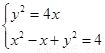 得
得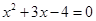 ,解得
,解得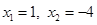
∵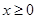 ,故
,故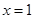 ,此时
,此时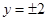 ;
故满足条件的点存在的,其坐标为
;
故满足条件的点存在的,其坐标为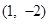 和
和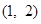
【解析】略

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
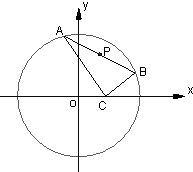 已知点C(1,0),点A、B是⊙O:x2+y2=9上任意两个不同的点,且满足
已知点C(1,0),点A、B是⊙O:x2+y2=9上任意两个不同的点,且满足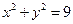 上任意两个不同的点,且满足
上任意两个不同的点,且满足 ,设P为弦AB的中点.
,设P为弦AB的中点. 的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.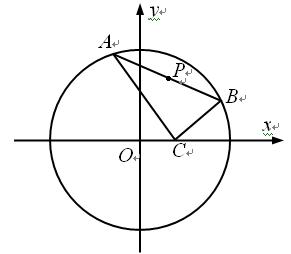
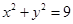 上任意两个不同的点,且满足
上任意两个不同的点,且满足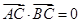 ,设P为弦AB的中点.
,设P为弦AB的中点.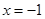 的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.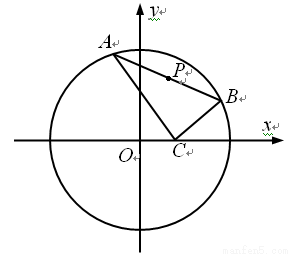
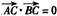 ,设P为弦AB的中点。
,设P为弦AB的中点。