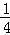题目内容
甲乙两人各自在300米长的直线形跑道上跑步,则在任一时刻两人在跑道上相距不超过50米的概率是多少( ).
A.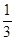 | B.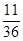 | C.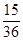 | D.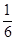 |
B
解析试题分析:由随机事件特点可知,甲乙两人可以在跑道上任何位置,且互不影响.同时考虑到两人距离不超过50米,将跑到建立数轴,且设甲乙两人的坐标为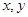 .则
.则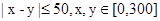 ,满足几何概型.
,满足几何概型.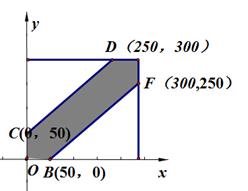
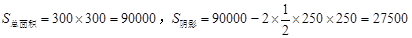 ,
,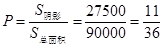 ,故B
,故B
考点:几何概型.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
设服从二项分布X~B(n,p)的随机变量X的均值与方差分别是15和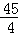 ,则n、p的值分别是( )
,则n、p的值分别是( )
A.50, | B.60, | C.50,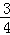 | D.60,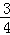 |
在独立性检验中,统计量 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当
 3.841时,认为两个事件无关,当
3.841时,认为两个事件无关,当 >6.635时,有99%的把握说明两个事件有关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
>6.635时,有99%的把握说明两个事件有关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的 =20.87,根据这一数据,认为打鼾与患心脏病之间( )
=20.87,根据这一数据,认为打鼾与患心脏病之间( )
| A.认为两者无关 | B.约有95%的打鼾者患心脏病 |
| C.有99%的把握认为两者有关 | D.约有99%的打鼾者患心脏病 |
已知随机变量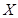 服从正态分布
服从正态分布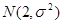 ,
,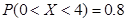 ,则
,则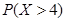 的值等于( )
的值等于( )
| A.0.1 | B.0.2 | C.0.4 | D.0.6 |
设随机变量 服从正态分布
服从正态分布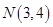 ,若
,若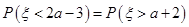 ,则
,则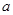 的值为( )
的值为( )
A.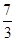 | B.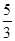 | C.5 | D.3 |
已知随机变量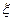 服从正态分布N(2,σ2),且P(
服从正态分布N(2,σ2),且P(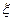 <4)=0.8,则P(0<
<4)=0.8,则P(0<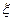 <2)=( )
<2)=( )
| A.0.6 | B.0.4 | C.0.3 | D.0.2 |