题目内容
已知椭圆的长轴长为2a,焦点是F1(-
,0),F2(
,0),点F1到直线x=-
的距离为
,过点F2且倾斜角为锐角的直线l与椭圆交于A,B两点,使得
=3
.
(1)求椭圆的方程;
(2)求直线l的方程.
| 3 |
| 3 |
| a2 | ||
|
| ||
| 3 |
| BF2 |
| F2A |
(1)求椭圆的方程;
(2)求直线l的方程.
分析:(1)首先由点F1到直线x=-
的距离为
列式求出a2的值,然后利用条件b2=a2-c2求出b2,则椭圆的方程可求;
(2)设出直线l与椭圆两个交点A,B的坐标,由
=3
得到两个交点坐标的关系式,把两个交点的坐标代入椭圆方程后可求其中一个交点的坐标,由两点式求出直线l的斜率,则直线l的方程可求.
| a2 | ||
|
| ||
| 3 |
(2)设出直线l与椭圆两个交点A,B的坐标,由
| BF2 |
| F2A |
解答:解:(1)∵F1到直线x=-
的距离为
,∴|-
+
|=
⇒a2=4.
而c2=3,∴b2=a2-c2=4-3=1,所求椭圆的方程为
+y2=1;
(2)设A(x1,y1),B(x2,y2),不妨设A为第一象限的点,且F2(
,0),
∵
=3
,∴
⇒
,
又∵A,B在椭圆
+y2=1上,∴
⇒
(取正值),
∴l的斜率为k=
=
.
∴l的方程为y=
(x-
),即
x-y-
=0.
| a2 | ||
|
| ||
| 3 |
| 3 |
| a2 | ||
|
| ||
| 3 |
而c2=3,∴b2=a2-c2=4-3=1,所求椭圆的方程为
| x2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),不妨设A为第一象限的点,且F2(
| 3 |
∵
| BF2 |
| F2A |
|
|
又∵A,B在椭圆
| x2 |
| 4 |
|
|
∴l的斜率为k=
| ||||||
|
| 2 |
∴l的方程为y=
| 2 |
| 3 |
| 2 |
| 6 |
点评:本题考查了椭圆标准方程的求法,考查了直线和圆锥曲线的交点问题,解答此题的关键是利用向量找到两交点坐标的关系,考查了学生的运算能力,训练了直线方程的点斜式,是中档题.

练习册系列答案
相关题目
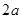 ,焦点是
,焦点是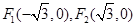 ,点
,点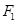 到直线
到直线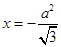 的距离为
的距离为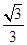 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线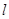 与椭圆交于
与椭圆交于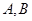 两点,使得
两点,使得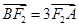 .
.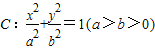 的长轴长为4.
的长轴长为4.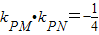 时,求椭圆的方程.
时,求椭圆的方程.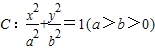 的长轴长为4.
的长轴长为4.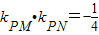 时,求椭圆的方程.
时,求椭圆的方程. 的长轴长为4.
的长轴长为4.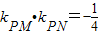 时,求椭圆的方程.
时,求椭圆的方程.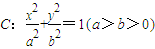 的长轴长为4.
的长轴长为4.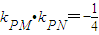 时,求椭圆的方程.
时,求椭圆的方程.