题目内容
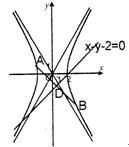
双曲线 的离心率e=2,F1,F2是左,右焦点,过F2作x轴的垂线与双曲线在第一象限交于P点,直线F1P与右准线交于Q点,已知
的离心率e=2,F1,F2是左,右焦点,过F2作x轴的垂线与双曲线在第一象限交于P点,直线F1P与右准线交于Q点,已知
(1)求双曲线的方程;
(2)设过F1的直线MN分别与左支,右支交于M、N,线段MN的垂线平分线l与x轴交于点G(x,0),若1≤|NF2|<3,求x的取值范围.
【答案】分析:(1)因为双曲线的离心率e=2,所以可得含a,c的等式,再由 ,可求出a值,结合a,b,c的关系式,就能求出b,双曲线的方程可知.
,可求出a值,结合a,b,c的关系式,就能求出b,双曲线的方程可知.
(2)因为直线MN过F1点,可设出点斜式方程,与与双曲线方程联立,求出两根之和,两根之积,再因为线段MN的垂线平分线l与MN斜率互为负倒数,且过MN中点,所以线段MN的垂线平分线l方程可以写出,再因为可用线段MN的垂线平分线l与x轴交于点G(x,0),可用含k的式子表示x,再根据1≤|NF2|<3,求x的范围即可.
解答:解:(1)∵e=2⇒c=2a,F1(-2a,0),F2(2a,0),P(2a,m)m=|PF2|=e•2a-a=3a∴P(2a,3a),
设Q ∵F1,Q,F2三点共线∴
∵F1,Q,F2三点共线∴ ∵
∵ 得a2=1
得a2=1
∴
(2)设MN:y=k(x+2)代入3x2-y2=3得:(3-k2)x2-4k2x-4k2-3=0△>0?k2+1>0
设M(x1,y1),N(x2,y2)
∵ ∴
∴
∵l过Q(x,0)∴ ∵|NF2|=2x1-1且|NF2|∈[1,3)
∵|NF2|=2x1-1且|NF2|∈[1,3)
∴x1∈[1,2) ⇒
⇒
令 ∵
∵
∴f(x1)在x1∈[1,2)上单调递增
得 ∵
∵ ∴
∴
点评:本题考查了双曲线方程的求法,以及直线与双曲线位置关系的判断,做题时要认真分析.
 ,可求出a值,结合a,b,c的关系式,就能求出b,双曲线的方程可知.
,可求出a值,结合a,b,c的关系式,就能求出b,双曲线的方程可知.(2)因为直线MN过F1点,可设出点斜式方程,与与双曲线方程联立,求出两根之和,两根之积,再因为线段MN的垂线平分线l与MN斜率互为负倒数,且过MN中点,所以线段MN的垂线平分线l方程可以写出,再因为可用线段MN的垂线平分线l与x轴交于点G(x,0),可用含k的式子表示x,再根据1≤|NF2|<3,求x的范围即可.
解答:解:(1)∵e=2⇒c=2a,F1(-2a,0),F2(2a,0),P(2a,m)m=|PF2|=e•2a-a=3a∴P(2a,3a),
设Q
 ∵F1,Q,F2三点共线∴
∵F1,Q,F2三点共线∴ ∵
∵ 得a2=1
得a2=1∴

(2)设MN:y=k(x+2)代入3x2-y2=3得:(3-k2)x2-4k2x-4k2-3=0△>0?k2+1>0
设M(x1,y1),N(x2,y2)
∵
 ∴
∴
∵l过Q(x,0)∴
 ∵|NF2|=2x1-1且|NF2|∈[1,3)
∵|NF2|=2x1-1且|NF2|∈[1,3)∴x1∈[1,2)
 ⇒
⇒
令
 ∵
∵
∴f(x1)在x1∈[1,2)上单调递增
得
 ∵
∵ ∴
∴
点评:本题考查了双曲线方程的求法,以及直线与双曲线位置关系的判断,做题时要认真分析.

练习册系列答案
相关题目
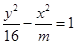 的离心率e=2,则m=____.
的离心率e=2,则m=____.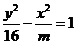 的离心率e=2,则m=____.
的离心率e=2,则m=____.