题目内容
(I)设a>0,b>0求证:a3+b3≥a2b+ab2
(II)设a>0,b>0,c>0,且a,b,c不且相等,求证:lg
+lg
+lg
>lga+lgb+lgc.
(II)设a>0,b>0,c>0,且a,b,c不且相等,求证:lg
| a+b |
| 2 |
| b+c |
| 2 |
| c+a |
| 2 |
证明:(Ⅰ)∵a3+b3-a2b-ab2=a2(a-b)-b2(a-b)=(a-b)2(a+b),
又a>0,b>0,
∴a+b>0,(a-b)2≥0,
∴(a-b)2(a+b)≥0,
∴a3+b3≥a2b+ab2;
(Ⅱ)∵a>0,b>0,c>0,
∴
≥
,
≥
,
≥
,
∴lg
≥lg
=
(lga+lgb)①,同理可得lg
≥
(lab+lgc)②,lg
≥
(lga+lgc)③,
①+②+③得:
lg
+lg
+lg
≥lga+lgb+lgc
又a,b,c不全相等,
∴lg
+lg
+lg
>lga+lgb+lgc.
又a>0,b>0,
∴a+b>0,(a-b)2≥0,
∴(a-b)2(a+b)≥0,
∴a3+b3≥a2b+ab2;
(Ⅱ)∵a>0,b>0,c>0,
∴
| a+b |
| 2 |
| ab |
| b+c |
| 2 |
| bc |
| a+c |
| 2 |
| ac |
∴lg
| a+b |
| 2 |
| ab |
| 1 |
| 2 |
| b+c |
| 2 |
| 1 |
| 2 |
| a+c |
| 2 |
| 1 |
| 2 |
①+②+③得:
lg
| a+b |
| 2 |
| b+c |
| 2 |
| c+a |
| 2 |
又a,b,c不全相等,
∴lg
| a+b |
| 2 |
| b+c |
| 2 |
| c+a |
| 2 |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

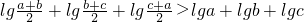 .
.