题目内容
已知函数y= 的定义域是A,函数y=
的定义域是A,函数y=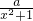 (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
解:若使函数y= 的解析式有意义
的解析式有意义
-x2+7x-12≥0
解得3≤x≤4
即A=[3,4]
∵y=x2+1的图象是开口朝上,且以y轴为对称轴的抛物线
故函数在[0,2]上为增函数
当a>0时,函数y=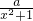 在[0,2]上为减函数
在[0,2]上为减函数
当x=0时,函数取最大值a,
当x=2时,函数取最小值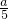 ,
,
故B=[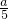 ,a]
,a]
由A⊆B
故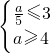 ,解得4≤a≤15
,解得4≤a≤15
故实数a的取值范围为[4,15]
分析:根据被开方数不小于0,解二次不等式求出集合A,根据二次函数的图象和性质,分析函数y=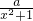 (a>0)在[0,2]上的单调性,进而求出函数的最值和值域求出B,结合A⊆B构造关于a的不等式组可得实数a的取值范围.
(a>0)在[0,2]上的单调性,进而求出函数的最值和值域求出B,结合A⊆B构造关于a的不等式组可得实数a的取值范围.
点评:本题以函数的值域,集合关系中的参数取值为载体考查了二次不等式及不等式组的解法,其中根据已知构造相应的不等式是解答的关键.
 的解析式有意义
的解析式有意义-x2+7x-12≥0
解得3≤x≤4
即A=[3,4]
∵y=x2+1的图象是开口朝上,且以y轴为对称轴的抛物线
故函数在[0,2]上为增函数
当a>0时,函数y=
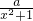 在[0,2]上为减函数
在[0,2]上为减函数当x=0时,函数取最大值a,
当x=2时,函数取最小值
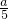 ,
,故B=[
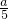 ,a]
,a]由A⊆B
故
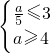 ,解得4≤a≤15
,解得4≤a≤15故实数a的取值范围为[4,15]
分析:根据被开方数不小于0,解二次不等式求出集合A,根据二次函数的图象和性质,分析函数y=
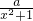 (a>0)在[0,2]上的单调性,进而求出函数的最值和值域求出B,结合A⊆B构造关于a的不等式组可得实数a的取值范围.
(a>0)在[0,2]上的单调性,进而求出函数的最值和值域求出B,结合A⊆B构造关于a的不等式组可得实数a的取值范围.点评:本题以函数的值域,集合关系中的参数取值为载体考查了二次不等式及不等式组的解法,其中根据已知构造相应的不等式是解答的关键.

练习册系列答案
相关题目
 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围. 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.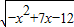 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.