题目内容
 对某校高一年级的学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,恨据此数据作出了右图所示的频数与频率的统计表和频率分布直方图:
对某校高一年级的学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,恨据此数据作出了右图所示的频数与频率的统计表和频率分布直方图:
| 分组 | 频数 | 频率 |
| [10,15) | 6 | 0.3 |
| [15,20) | 8 | N |
| [20,25) | M | P |
| [25,30) | 2 | 0.1 |
| 合计 | M | 1 |
(II)学校诀定对参加社区服务的学生进行表彰,对参加活动次数在[25,30]区间的每个学生发放价值80元的学习用品,对参加活动次数在[15,20)区间的每个学生发放价值40元的学习用品,对参加活动次数在[10,15)区间的每个学生发放价值20元的学习用品,在所抽取的这M名学生中,任意取出2人,设X为此二人所获得学习用品价值之差的绝对值,求X的分布列与数学期望E(X).
解:(Ⅰ)由题可知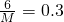 ,
,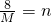 ,
,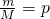 ,
, ,
,
又6+8+m+2=M,
解得M=20,n=0.4,m=4,p=0.2,
故[15,20)组的频率与组距之比a为0.08.(4分)
(Ⅱ)可知X的值可能为0元、20元、40元、60元,(5分)
则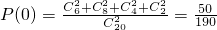 ,
, ,
,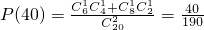 ,
,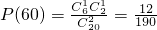 .(9分)
.(9分)
所以X的分布列为:
(10分)
 .(12分)
.(12分)
分析:(I)根据频率的定义列式并解之,可得M=20且n=0.4,再根据各组频率之和等于1,算出p和m的值,最后根据直方图的定义可得a的值;
(II)确定X的取值,求出相应的概率,可得X的分布列与数学期望E(X).
点评:本题以频率分布直方图为载体,考查了频率的定义、直方图的含义,考查离散型随机变量的分布列与期望,属于中档题.
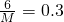 ,
,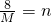 ,
,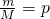 ,
, ,
,又6+8+m+2=M,
解得M=20,n=0.4,m=4,p=0.2,
故[15,20)组的频率与组距之比a为0.08.(4分)
(Ⅱ)可知X的值可能为0元、20元、40元、60元,(5分)
则
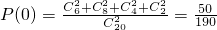 ,
, ,
,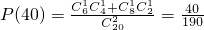 ,
,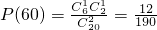 .(9分)
.(9分)所以X的分布列为:
| X | 0 | 20 | 40 | 60 |
| P | 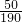 |  |  |  |
 .(12分)
.(12分)分析:(I)根据频率的定义列式并解之,可得M=20且n=0.4,再根据各组频率之和等于1,算出p和m的值,最后根据直方图的定义可得a的值;
(II)确定X的取值,求出相应的概率,可得X的分布列与数学期望E(X).
点评:本题以频率分布直方图为载体,考查了频率的定义、直方图的含义,考查离散型随机变量的分布列与期望,属于中档题.

练习册系列答案
相关题目
对某校高一年级的学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,恨据此数据作出了如图所示的频数与频率的统计表和频率分布直方图:
(I)求出表中M、p及图中a的值;
(II)学校诀定对参加社区服务的学生进行表彰,对参加活动次数在[25,30)区间的每个学生发放价值80元的学习用品,对参加活动次数在[20,25)区间的每个学生发放价值60元的学习用品,对参加活动次数在[15,20)区间的每个学生发放价值40元的学习用品,对参加活动次数在[10,15)区间的每个学生发放价值20元的学习用品,在所抽取的这M名学生中,任意取出2人,求此二人所获得学习用品价值之差的绝对值不超过20元的概率.
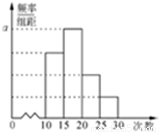
| 分组 | 频数 | 频率 |
| [10,15) | 6 | 0.3 |
| [15,20) | 8 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.1 |
| 合计 | M | 1 |
(II)学校诀定对参加社区服务的学生进行表彰,对参加活动次数在[25,30)区间的每个学生发放价值80元的学习用品,对参加活动次数在[20,25)区间的每个学生发放价值60元的学习用品,对参加活动次数在[15,20)区间的每个学生发放价值40元的学习用品,对参加活动次数在[10,15)区间的每个学生发放价值20元的学习用品,在所抽取的这M名学生中,任意取出2人,求此二人所获得学习用品价值之差的绝对值不超过20元的概率.

 (2012•资阳三模)对某校高一年级的学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,恨据此数据作出了右图所示的频数与频率的统计表和频率分布直方图:
(2012•资阳三模)对某校高一年级的学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,恨据此数据作出了右图所示的频数与频率的统计表和频率分布直方图: (2012•资阳三模)对某校高一年级的学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,恨据此数据作出了如图所示的频数与频率的统计表和频率分布直方图:
(2012•资阳三模)对某校高一年级的学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,恨据此数据作出了如图所示的频数与频率的统计表和频率分布直方图: