题目内容
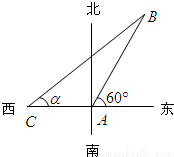
 如图,某军舰艇位于岛屿A的正西方C处,且与岛屿A相距120海里.经过侦察发现,国际海盗艇以100海里/小时的速度从岛屿A出发沿东偏北60°方向逃窜,同时,该军舰艇从C处出发沿东偏北α的方向匀速追赶国际海盗船,恰好用2小时追上.
如图,某军舰艇位于岛屿A的正西方C处,且与岛屿A相距120海里.经过侦察发现,国际海盗艇以100海里/小时的速度从岛屿A出发沿东偏北60°方向逃窜,同时,该军舰艇从C处出发沿东偏北α的方向匀速追赶国际海盗船,恰好用2小时追上.(1)求该军舰艇的速度;
(2)求sinα的值.
分析:(1)依题意知,∠CAB=120°,AB=100×2=200,AC=120,∠ACB=α,在△ABC中,由余弦定理求得BC的值,从而求得该军舰艇的速度.
(2)在△ABC中,由正弦定理,可得
=
,由此可得sinα的值.
(2)在△ABC中,由正弦定理,可得
| AB |
| sinα |
| BC |
| sin120° |
解答:解:(1)依题意知,∠CAB=120°,AB=100×2=200,AC=120,∠ACB=α,
在△ABC中,由余弦定理得
BC2=AB2+AC2-2AB•ACcos∠CAB=2002+1202-2×200×120cos120°=78400,
解得BC=280,所以,该军舰艇的速度为
=140 (海里/小时).
(2)在△ABC中,由正弦定理,可得
=
,
求得 sinα=
=
=
.
在△ABC中,由余弦定理得
BC2=AB2+AC2-2AB•ACcos∠CAB=2002+1202-2×200×120cos120°=78400,
解得BC=280,所以,该军舰艇的速度为
| BC |
| 2 |
(2)在△ABC中,由正弦定理,可得
| AB |
| sinα |
| BC |
| sin120° |
求得 sinα=
| ABsin120° |
| BC |
200×
| ||||
| 280 |
5
| ||
| 14 |
点评:本题主要考查正弦定理、余弦定理的应用,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 如图,某海滨城市位于海岸A处,在城市A的南偏西20°方向有一个海面观测站B,现测得与B处相距31海里的C处,有一艘豪华游轮正沿北偏西40°方向,以40海里/小时的速度向城市A直线航行,30分钟后到达D处,此时测得B、D间的距离为21海里.
如图,某海滨城市位于海岸A处,在城市A的南偏西20°方向有一个海面观测站B,现测得与B处相距31海里的C处,有一艘豪华游轮正沿北偏西40°方向,以40海里/小时的速度向城市A直线航行,30分钟后到达D处,此时测得B、D间的距离为21海里.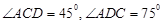 ,目标出现于地面点B处时,测得
,目标出现于地面点B处时,测得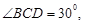
 ,求炮兵阵地到目标的距离。
,求炮兵阵地到目标的距离。