题目内容
复数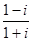 与复数
与复数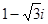 在复平面上所对应的向量分别是
在复平面上所对应的向量分别是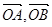 ,
,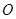 为原点,则这两个向量的夹角
为原点,则这两个向量的夹角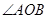 等于( )
等于( )
A.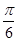 | B.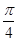 | C.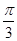 | D.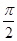 |
A
解析试题分析:根据题意,由于复数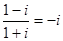 与复数
与复数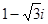 ,在复平面上所对应的向量分别是
,在复平面上所对应的向量分别是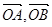 ,分别与x轴所成的角为
,分别与x轴所成的角为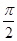 ,
,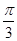 ,那么根据复数的几何意义,可知这两个向量的夹角
,那么根据复数的几何意义,可知这两个向量的夹角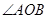 等于
等于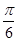 ,故选A.
,故选A.
考点:复数的几何意义
点评:解决该试题的关键是利用复数的几何意义得到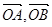 与x轴的所成的夹角,属于基础题。
与x轴的所成的夹角,属于基础题。

练习册系列答案
相关题目
复数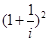 的虚部是
的虚部是
A. | B.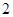 | C.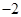 | D.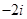 |
i 是虚数单位,复数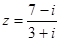 =( )
=( )
A.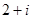 | B.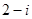 | C.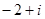 | D.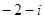 |
若复数 是纯虚数(
是纯虚数(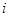 是虚数单位),则
是虚数单位),则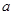 的值为 ( )
的值为 ( )
A. | B. | C.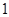 | D. |
已知复数 ,
, ,则
,则 对应点位于复平面的( )
对应点位于复平面的( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
下面给出了关于复数的四种类比推理:
①复数的加减法运算可以类比多项式的加减法运算法则;
②由向量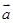 的性质
的性质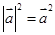 类比得到复数
类比得到复数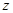 的性质
的性质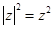 ;
;
③方程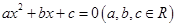 有两个不同实数根的条件是
有两个不同实数根的条件是 可以类比得到:方程
可以类比得到:方程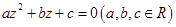 有两个不同复数根的条件是
有两个不同复数根的条件是 ;
;
④由向量加法的几何意义可以类比得到复数加法的几何意义
其中类比得到的结论错误的是
| A.①③ | B.②④ | C.②③ | D.①④ |
若复数 (
( 为虚数单位)是纯虚数,则实数
为虚数单位)是纯虚数,则实数 的值为 ( )
的值为 ( )
| A.6 | B.-6 | C.5 | D.-4 |
复数 的虚部是( )
的虚部是( )
A. | B. | C. | D. |
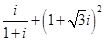 对应的点位于( )
对应的点位于( )