题目内容
某港口的水深(米)是时间t(0≤t≤24)(单位:时)的函数,记作y=f(t)下面是该港口某季节每天水深的数据:
经过长期观察,y=f(t)的曲线可近似地看作y=Asinωt+b的图象,一般情况下,船舶航行时,船底离海底的距离不小于5m是安全的(船舶停靠岸时,船底只需不碰海底即可).某船吃水深度(船底离水面距离)为6.5m,如果该船想在同一天内安全出港,问它至多能在港内停留的时间是(忽略进出港所用时间)( )
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 10.0 | 13.0 | 10.01 | 7.0 | 10.0 | 13.0 | 10.01 | 7.0 | 10.0 |
| A、17 | B、16 | C、5 | D、4 |
分析:寻求变量之间的关系是解题的关键.引进角,利用三角函数的定义,易得变量之间的关系,其模型是三角函数.
解答:解:由已知数据,易知y=f(t)的周期T=12,振幅A=13-10=3,b=10,所以y=3sin
t+10;
由该船进出港时,水深应不小于5+6.5=11.5(m),∴3sin
t+10≥11.5,
即
+2kπ≤
t≤
+2kπ(k∈Z),
∴12k+1≤t≤12k+5(k∈Z),在同一天内,取k=0或1,
所以1≤t≤5或13≤t≤17.
故该船可在当日凌晨1时进港,17时离港,它在港内至多停留16小时.
| π |
| 6 |
由该船进出港时,水深应不小于5+6.5=11.5(m),∴3sin
| π |
| 6 |
即
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴12k+1≤t≤12k+5(k∈Z),在同一天内,取k=0或1,
所以1≤t≤5或13≤t≤17.
故该船可在当日凌晨1时进港,17时离港,它在港内至多停留16小时.
点评:求解具有周期变化现象的实际问题关键是能抽象出三角函数模型,解决的步骤是:审题,建模,求解,还原.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
(本小题满分10分)某港口的水深 (米)是时间
(米)是时间 (
(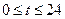 ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
 | 10 | 13 | 9.9 | 7 | 10 | 13 | 10.1 | 7 | 10 |
 可近似的看成是函数
可近似的看成是函数
(1)根据以上数据,求出
 的解析式
的解析式(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
(本小题满分10分)某港口的水深 (米)是时间
(米)是时间 (
( ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测,  可近似的看成是函数
可近似的看成是函数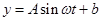
(1)根据以上数据,求出 的解析式
的解析式
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
某港口的水深 (米)是时间
(米)是时间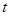 (
( ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测,  可近似的看成是函数
可近似的看成是函数 ,(本小题满分14分)
,(本小题满分14分)
(1)根据以上数据,求出 的解析式。
的解析式。
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
【解析】第一问由表中数据可以看到:水深最大值为13,最小值为7,,
∴A+b=13, -A+b=7 解得 A=3, b=10
第二问要想船舶安全,必须深度 ,即
,即
∴

解得:
 得到结论。
得到结论。

