题目内容
点P是椭圆16x2+25y2=1600上一点,F1、F2是椭圆的两个焦点,又知点P在x轴上方,F2为椭圆的右焦点,直线PF2的斜率为-4| 3 |
分析:将椭圆的方程转化为标准形式,求出两个焦点的坐标,利用点斜式求出直线的方程,将椭圆方程与直线的方程联立求出交点的坐标,利用三角形的面积底乘高除以2求出三角形的面积.
解答:解:F1、F2是椭圆
+
=1的左、右焦点,
则F1(-6,0),F2(6,0),
设P(x,y)是椭圆上一点,则
消去y,得19x2-225x+6500=0,
得x1=5或x2=
当x2=
时,代入(2)得y2=-
与(3)矛盾,舍去.
由x=5,得y=4
.
所以,△PF1F2的面积S=
|F1F2|•h=
×12×4
=24
.
| x2 |
| 100 |
| y2 |
| 64 |
则F1(-6,0),F2(6,0),
设P(x,y)是椭圆上一点,则
|
消去y,得19x2-225x+6500=0,
得x1=5或x2=
| 130 |
| 19 |
当x2=
| 130 |
| 19 |
64
| ||
| 19 |
由x=5,得y=4
| 3 |
所以,△PF1F2的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:解决直线与圆锥曲线的位置关系问题,一般将直线的方程与椭圆的方程联立,消去一个未知数得到关于一个未知数的方程,利用韦达定理得到交点坐标的关系找突破口.

练习册系列答案
相关题目
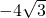 :求△PF1F2的面积.
:求△PF1F2的面积.