题目内容
①.已知函数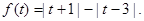 则
则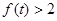 的解为
的解为
②. 在直角坐标系中,直线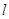 的参数方程为
的参数方程为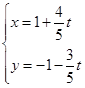 (
(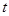 为参数),若以
为参数),若以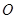 为极点,
为极点, 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线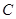 的极坐标方程为
的极坐标方程为 ,则直线
,则直线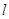 被曲线
被曲线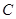 所截得的弦长为
所截得的弦长为
(1)t>2 (2)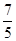
解析试题分析:①通过分类讨论,将f(t)中的绝对值符号去掉,解不等式组即可;
②将直线l的参数方程与圆的极坐标方程转化为普通方程,由弦长公式即可求得直线l被曲线C所截得的弦长.
考点:绝对值不等式的解法;简单曲线的极坐标方程;参数方程化成普通方程.
点评:本题考查绝对值不等式的解法,考查简单曲线的极坐标方程与直线的参数方程,考查转化思想与运算能力.

练习册系列答案
相关题目
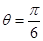 (
(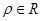 )截圆
)截圆 所得弦长是 .
所得弦长是 . ,曲线
,曲线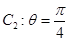 ,若曲线
,若曲线 与
与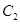 交于
交于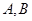 两点,则线段
两点,则线段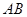 的长度为
的长度为 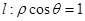 被圆
被圆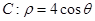 所截得的线段长为________.
所截得的线段长为________. 与直线l关于 直线θ=
与直线l关于 直线θ= (ρ∈R)对称,则l的极坐标方程是 .
(ρ∈R)对称,则l的极坐标方程是 .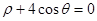 的圆心位置后顺时针方向旋转60o后直线方向到达圆周
的圆心位置后顺时针方向旋转60o后直线方向到达圆周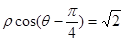 与圆
与圆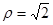 的公共点个数是________.
的公共点个数是________.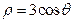 ,则圆截直线
,则圆截直线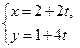 (
(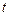 是参数
是参数 所得的弦长为______
所得的弦长为______ 围成的面积是
围成的面积是