题目内容
设M是由满足下列条件的函数f(x)构成的集合:“①方程f(x)﹣x=0有实数根;②函数f(x)的导数f′(x)满足0<f′(x)<1.”
(I)判断函数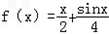 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素f(x)具有下面的性质:若f(x)的定义域为D,则对于任意
[m,n]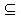 D,都存在x0∈(m,n),使得等式f(n)﹣f(m)=(n﹣m)f'(x0)成立.
D,都存在x0∈(m,n),使得等式f(n)﹣f(m)=(n﹣m)f'(x0)成立.
试用这一性质证明:方程f(x)﹣x=0只有一个实数根;
(III)设x1是方程f(x)﹣x=0的实数根,求证:对于f(x)定义域中任意的x2,x3,当|x2﹣x1|<1,且|x3﹣x1|<1时,有|f(x3)﹣f(x2)|<2.
(I)判断函数
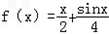 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;(II)集合M中的元素f(x)具有下面的性质:若f(x)的定义域为D,则对于任意
[m,n]
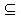 D,都存在x0∈(m,n),使得等式f(n)﹣f(m)=(n﹣m)f'(x0)成立.
D,都存在x0∈(m,n),使得等式f(n)﹣f(m)=(n﹣m)f'(x0)成立.试用这一性质证明:方程f(x)﹣x=0只有一个实数根;
(III)设x1是方程f(x)﹣x=0的实数根,求证:对于f(x)定义域中任意的x2,x3,当|x2﹣x1|<1,且|x3﹣x1|<1时,有|f(x3)﹣f(x2)|<2.
解:(I)因为 ,
,
又因为当x=0时,f(0)=0,
所以方程f(x)﹣x=0有实数根0.
所以函数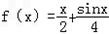 是的集合M中的元素.
是的集合M中的元素.
(II)假设方程f(x)﹣x=0存在两个实数根α,β(α≠β),
则f(α)﹣α=0,f(β)﹣β=0
不妨设α<β,
根据题意存在数c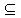 (α,β)使得等式f(β)﹣f(α)=(β﹣α)f'(c)成立.
(α,β)使得等式f(β)﹣f(α)=(β﹣α)f'(c)成立.
因为f(α)=α,f(β)=β,且α≠β,
所以f'(c)=1,与已知0<f'(x)<1矛盾,
所以方程f(x)﹣x=0只有一个实数根;
(III)不妨设x2<x3,
因为f'(x)>0,所以f(x)为增函数,
所以f(x2)<f(x3),
又因为f'(x)﹣1<0,所以函数f(x)﹣x为减函数,
所以f(x2)﹣x2>f(x3)﹣x3,
所以0<f(x3)﹣f(x2)<x3﹣x2,即|f(x3)﹣f(x2)|<|x3﹣x2|,
所以|f(x3)﹣f(x2)|<|x3﹣x2|=|x3﹣x1﹣(x2﹣x1)|≤|x3﹣x1|+|x2﹣x1|<2

练习册系列答案
相关题目