题目内容
已知函数f(x)=(x+1)2
(1)当1≤x≤m时,不等式f(x-3)≤x恒成立,求实数m的最大值;
(2)在曲线y=f(x+t)上存在两点关于直线y=x对称,求t的取值范围;
(3)在直线![]() 上取一点P,过P作曲线y=f(x+t)的两条切线l1、l2,求证:l1⊥l2
上取一点P,过P作曲线y=f(x+t)的两条切线l1、l2,求证:l1⊥l2
答案:
解析:
解析:
|
解:(1)直线y=x与曲线 求得交点为(1,1)和(4,4),此时 (2)设曲线上关于直线y=x的对称点为A( 又因为AB中点在直线y=x上,所以 得 (3)设P的坐标为 则有 直线 则 |

练习册系列答案
相关题目
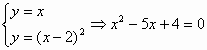
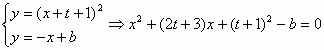
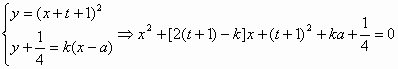
 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有