题目内容
从2008年9月12日含有三聚氰胺的“三鹿”婴儿毒奶粉事件曝光后,国家质检部门加大了对各种乳制品的检查力度.现随机抽取某品牌乳制品企业的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为ξ.(Ⅰ)求ξ的分布列及1件产品的平均利润;
(Ⅱ)为了提高乳制品的质量,国内某名牌乳制品企业经技术革新,虽然仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,求三等品率最多是多少?
【答案】分析:(I)求出ξ的所有取值以及ξ取每一个值的概率值,列出分布列,利用随机变量的期望公式求出1件产品的平均利润;
(II)设三等品率最多为x,列出随机变量ξ的分布列,利用随机变量的期望公式列出关于x的不等式,求出x的范围.
解答:(Ⅰ)ξ的取值:6、2、1、-2…(1分)
P(ξ=6)=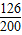 =0.63;P(ξ=2)=
=0.63;P(ξ=2)=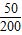 =0.25;
=0.25;
P(ξ=1)=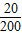 =0.1;P(ξ=-2)=
=0.1;P(ξ=-2)=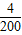 =0.02; …(4分)
=0.02; …(4分)
ξ的分布列:
Eξ=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34…(6分)
(Ⅱ)设三等品率最多为x.
…(9分)
Eξ=6×0.7+2×(0.29-x)+1×x+(-2)×0.01≥4.73
∴x≤0.03
∴三等品率最多为3% …12分)
点评:本题主要考查了离散型随机变量及其分布列和离散型随机变量的期望与方差,属于基础题之列.
(II)设三等品率最多为x,列出随机变量ξ的分布列,利用随机变量的期望公式列出关于x的不等式,求出x的范围.
解答:(Ⅰ)ξ的取值:6、2、1、-2…(1分)
P(ξ=6)=
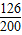 =0.63;P(ξ=2)=
=0.63;P(ξ=2)=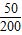 =0.25;
=0.25;P(ξ=1)=
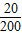 =0.1;P(ξ=-2)=
=0.1;P(ξ=-2)=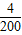 =0.02; …(4分)
=0.02; …(4分)ξ的分布列:
| ξ | 6 | 2 | 1 | -2 |
| P | 0.63 | 0.25 | 0.1 | 0.02 |
(Ⅱ)设三等品率最多为x.
| ξ | 6 | 2 | 1 | -2 |
| P | 0.7 | 0.29-x | x | 0.01 |
Eξ=6×0.7+2×(0.29-x)+1×x+(-2)×0.01≥4.73
∴x≤0.03
∴三等品率最多为3% …12分)
点评:本题主要考查了离散型随机变量及其分布列和离散型随机变量的期望与方差,属于基础题之列.

练习册系列答案
相关题目