题目内容
设椭圆
上的一点P到直线y=3，x=4的距离分别为d1，d2，则2d1+d2的最小值为
- A.5
- B.6
- C.7
- D.8
B
分析：根据题意有2d1+d2=2（3-y）+（4-x）=10-2y-x，再用三角函数表示坐标，从而利用三角函数的有界性求最小值．
解答：设P（x，y），则2d1+d2=2（3-y）+（4-x）=10-2y-x，
再令P（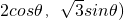
，则2d1+d2=10-
，
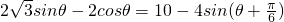∴2d1+d2的最小值为6，
故选B．
点评：本题主要考查点线距离，考查点的坐标的假设方法，关键是利用三角函数表示坐标，从而求函数的最值．
分析：根据题意有2d1+d2=2（3-y）+（4-x）=10-2y-x，再用三角函数表示坐标，从而利用三角函数的有界性求最小值．
解答：设P（x，y），则2d1+d2=2（3-y）+（4-x）=10-2y-x，
再令P（
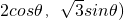，则2d1+d2=10-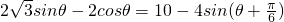，∴2d1+d2的最小值为6，
故选B．
点评：本题主要考查点线距离，考查点的坐标的假设方法，关键是利用三角函数表示坐标，从而求函数的最值．
练习册系列答案
相关题目
上的一点P到直线3x＋4y－12=0的距离为
，则满足条件的点P的个数为________．