题目内容
函数 的部分图象如图所示,则此函数的解析式为( )
的部分图象如图所示,则此函数的解析式为( )
A. | B. |
C. | D. |
A
解析试题分析:根据题意,图像中最大值和最小值分别为2,-2,那么A=2,同时可知2(4-1)=6,是二分之一周期的长度,因此一个周期的长度为6,因此 ,然后代入点(1,0),可知,f(1)=0,则可知0=2sin(
,然后代入点(1,0),可知,f(1)=0,则可知0=2sin(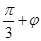 ),那么可得
),那么可得 符合题意。故选A.
符合题意。故选A.
考点:本试题主要是考查了三角函数的解析式的求解运用。
点评:解决这类问题的关键是能通过结合图像来得到振幅,从而得到A,再结合周期得到w,对于 的求解,代入一个特殊点然后解方程即可。熟练的理解三个参数与三角函数性质之间的关系运用。属于基础题。
的求解,代入一个特殊点然后解方程即可。熟练的理解三个参数与三角函数性质之间的关系运用。属于基础题。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
函数 的递增区间是
的递增区间是
A. | B. | C. | D. |
已知 ,则点
,则点 位于( )
位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
为了得到函数 的图像,只要把函数
的图像,只要把函数 图象上所有的点( )
图象上所有的点( )
A.向左平行移动 个单位长度 个单位长度 | B.向右平行移动 个单位 个单位 |
C.向左平行移动 个单位长度 个单位长度 | D.向右平行移动 个单位 个单位 |
已知 =
= ,0<x<π,则tanx为( )
,0<x<π,则tanx为( )
A.- | B.- | C.2 | D.-2 |
曲线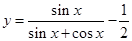 在点
在点 处的切线的斜率为( )
处的切线的斜率为( )
A. | B. | C. | D. |
已知函数 (
( )的周期为
)的周期为 ,在一个周期内的图象如图所示,则正确的结论是( )
,在一个周期内的图象如图所示,则正确的结论是( )
A. | B. |
C. | D. |
函数 =
=
 R)
R) 的部分图像如图所示,如果
的部分图像如图所示,如果 ,且
,且 ,则
,则

A. | B. | C. | D.1 |
若关于x的不等式 在闭区间
在闭区间 上恒成立,则实数
上恒成立,则实数 的取值范围是:( )
的取值范围是:( )
A. | B. | C. | D. |