题目内容
已知奇函数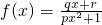 有最大值
有最大值 ,且
,且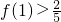 ,其中实数x>0,p、q是正整数..
,其中实数x>0,p、q是正整数..
(1)求f(x)的解析式;
(2)令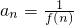 ,证明an+1>an(n是正整数).
,证明an+1>an(n是正整数).
解:(1)由奇函数f(-x)=-f(x)可得r=0,
x>0时,由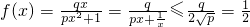 ①
①
以及 ②
②
可得到2q2-5q+2<0,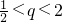 ,只有q=1=p,
,只有q=1=p,
∴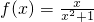 ;
;
(2)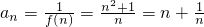 ,
,
则由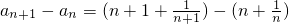
=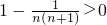 (n是正整数),
(n是正整数),
可得所求证结论.
分析:(1)由奇函数的定义知f(-x)+f(x)=0恒成立,求出r,利用基本不等式求出函数的最大值,以及且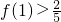 ,其中p、q是正整数,即得函数的解析式.
,其中p、q是正整数,即得函数的解析式.
(2)根据(1),求出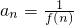 ,作出,即可证明结论.
,作出,即可证明结论.
点评:本题是中档题.考查函数的奇偶性和函数的最值,以及待定系数法求函数的解析式,以一道不错的综合题,考查分析问题解决问题的能力和运算能力.
x>0时,由
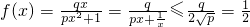 ①
①以及
 ②
②可得到2q2-5q+2<0,
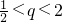 ,只有q=1=p,
,只有q=1=p,∴
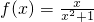 ;
;(2)
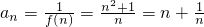 ,
,则由
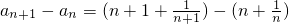
=
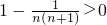 (n是正整数),
(n是正整数),可得所求证结论.
分析:(1)由奇函数的定义知f(-x)+f(x)=0恒成立,求出r,利用基本不等式求出函数的最大值,以及且
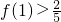 ,其中p、q是正整数,即得函数的解析式.
,其中p、q是正整数,即得函数的解析式.(2)根据(1),求出
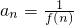 ,作出,即可证明结论.
,作出,即可证明结论.点评:本题是中档题.考查函数的奇偶性和函数的最值,以及待定系数法求函数的解析式,以一道不错的综合题,考查分析问题解决问题的能力和运算能力.

练习册系列答案
相关题目