Question

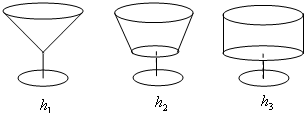
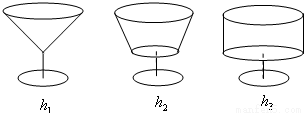
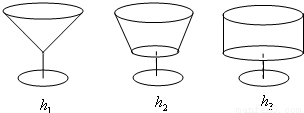
三位学友在一次聚会上，他们按照各自的爱好选取了形状不同、内空高度相等、杯口半径相等的圆口饮料杯，如图所示．盛满饮料后约定：先各自饮杯中饮料一半．设剩余饮料的高度从左到右依次为h₁，h₂，h₃，则它们的大小关系是

h₁＞h₂＞h₃

．

Answer 1

分析：由于形状不同、内空高度相等、杯口半径相等的圆口饮料杯，直接结合图形，判断三个几何体剩余饮料的高度即可．

解答：解：由于形状不同、内空高度相等、杯口半径相等的圆口饮料杯，
圆锥、圆柱是圆台的特例，故h₂介于h₁，h₃之间；
圆锥的上部一半的饮料是倒放圆台，圆台的下底面是下部饮料圆锥的底面，
所以h₁的高度大于

1

2

，
所以结论是h₁＞h₂＞h₃．
故答案为：h₁＞h₂＞h₃．

点评：本题是基础题，考查圆锥，圆柱，圆台的体积的计算，考查学生分析问题解决问题的能力．