Question

2．如图，三棱柱ABC-A₁B₁C₁中，∠ACB=90°，AC=BC=CC₁=2，A₁B⊥B₁C
（Ⅰ）证明：A₁C₁⊥CC₁
（Ⅱ）若A₁B=2$\sqrt{3}$，在棱CC₁上是否存在点E，使得二面角E-AB₁-C的大小为30°若存在，求CE的长，若不存在，说明理由．

Answer 1

分析 （Ⅰ）根据线面垂直的性质证明A₁C₁⊥平面CBB₁C₁ 即可证明：A₁C₁⊥CC₁
（Ⅱ）建立空间坐标系，求出平面的法向量，利用向量法进行求解即可．

解答 （Ⅰ）证明：连接BC₁
∵BCC₁B₁为平行四边形，且BC=CC₁=2，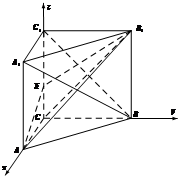
∴BCC₁B₁为菱形，
∴BC₁⊥B₁C …（2分）
又∵A₁B⊥B₁C，
∴B₁C⊥平面A₁C₁B
∴B₁C⊥A₁C₁，…（4分）
又∵AC⊥CB，
∴A₁C₁⊥C₁B₁
∴A₁C₁⊥平面CBB₁C₁  
∴A₁C₁⊥CC₁，…（6分）
（Ⅱ）∵A₁B=2$\sqrt{3}$，A₁C₁=2，
∴BC₁=2$\sqrt{2}$，
∴CC₁⊥BC
∴AC，CB，CC₁两两垂直…（8分）
以C为坐标原点，CA的方向为x轴的正方向建立空间直角坐标系C-xyz，
如图所示，则C（0，0，0），A（2，0，0），B₁（0，2，2），C₁（0，0，2），B（0，2，0），
设E（0，0，a），
则$\overrightarrow{AE}$=（-2，0，a），$\overrightarrow{A{B}_{1}}$=（-2，2，2），$\overrightarrow{B{C}_{1}}$=（0，-2，2），
易知，BC₁⊥平面AB₁C，
则平面AB₁C的一个法向量$\overrightarrow{m}$=（0，-1，1）
设$\overrightarrow{n}$=（x，y，1）是平面AB₁E的一个法向量
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=-2x+a=0}\\{\overrightarrow{n}•\overrightarrow{A{B}_{1}}=-2x+2y+2=0}\end{array}\right.$，
得$\overrightarrow{n}$=（$\frac{a}{2}$，$\frac{a}{2}$-1，1）…（10分）
则|cos＜$\overrightarrow{m}$，$\overrightarrow{n}$＞|=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{|\frac{a}{2}-2|}{\sqrt{2}•\sqrt{（\frac{a}{2}）^{2}+（\frac{a}{2}-1）^{2}+1}}$=$\frac{\sqrt{3}}{2}$，
解得：a=1，
∴在棱CC₁上存在点E，当CE=1时，得二面角E-AB₁-C的大小为30°．…（12分）

点评 本题主要考查空间直线垂直的证明以及空间二面角的大小的求解，利用坐标系结合向量法是解决本题的关键．