题目内容
在抛物线y=x2上依次取两点,它们的横坐标分别为x1=1,x2=3,若抛物线上过点P的切线与过这两点的割线平行,则P点的坐标为分析:把x1=1,x2=3代入抛物线方程可分别求得两点的纵坐标,进而求得割线的斜率,然后对抛物线方程进行求导,利用切线斜率为4求得x的值,把x的值代入抛物线方程进去求得P点的坐标.
解答:解:把x1=1,x2=3代入抛物线方程求得y1=1,y2=9
∴割线斜率k=
=4
对抛物线方程求导得y'=2x
∵抛物线上过点P的切线与过这两点的割线平行,
∴2x=4,x=2
把x=2代入抛物线方程求得y=4
∴P点为(2,4)
故答案为:(2,4)
∴割线斜率k=
| 9-1 |
| 3-1 |
对抛物线方程求导得y'=2x
∵抛物线上过点P的切线与过这两点的割线平行,
∴2x=4,x=2
把x=2代入抛物线方程求得y=4
∴P点为(2,4)
故答案为:(2,4)
点评:本题主要考查了抛物线的简单性质,直线与圆锥曲线的位置关系.考查了综合分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的焦点为F1.
的焦点为F1. ,又因为
,又因为 ,这样可知得到
,这样可知得到 。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到
。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到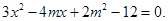 ,再利用
,再利用 可以结合韦达定理求解得到m的值和圆p的方程。
可以结合韦达定理求解得到m的值和圆p的方程。
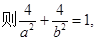 ①………………………………1分
①………………………………1分
 ………………………7分
………………………7分 、
、 ………………8分
………………8分
 ………………………9分
………………………9分 ……………………………10分
……………………………10分