题目内容
若函数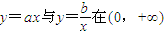
上都是减函数，则y=ax2+bx在（-∞，0）上是（ ）A．增函数
B．减函数
C．先增后减
D．先减后增
【答案】分析：根据正比例函数和反比例函数的图象和性质，可以求出a，b的值，进而求出函数y=ax2+bx的解析式，再由二次函数的图象和性质可以得到结论．
解答：解：∵函数
上都是减当函数，
∴a＜0，b＞0
故函数y=ax2+bx的图象是开口朝下且对称轴在Y轴右侧的抛物线
故y=ax2+bx在（-∞，0）上是增函数
故选A
点评：本题考查的知识点是函数的单调性的性质，熟练掌握基本初等函数的图象和性质是解答本题的关键．
解答：解：∵函数
上都是减当函数，∴a＜0，b＞0
故函数y=ax2+bx的图象是开口朝下且对称轴在Y轴右侧的抛物线
故y=ax2+bx在（-∞，0）上是增函数
故选A
点评：本题考查的知识点是函数的单调性的性质，熟练掌握基本初等函数的图象和性质是解答本题的关键．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
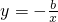在（0，+∞）上都是减函数，对函数y=ax3+bx的单调性描述正确的是
上都是减函数，则函数
上是（ ）