题目内容
8.分别求适合下列条件的直线方程:(1)经过点P(3,2),且在两坐标轴上的截距相等;
(2)过点A(1,-1)与已知直线l:2x+y-6=0相交于B点,且|AB|=5.
分析 (1)当直线过原点时,符合题意;当直线不过原点时设方程为$\frac{x}{a}$+$\frac{y}{a}$=1,代点求a可得;
(2)当直线斜率不存在时,符合题意;
当直线有斜率时,设直线方程为y+1=k(x-1),联立方程组解交点,由距离公式可得k的方程,解方程可得.
解答 解:(1)当直线过原点时方程为y=$\frac{2}{3}$x,即2x-3y=0,符合题意;
当直线不过原点时设方程为$\frac{x}{a}$+$\frac{y}{a}$=1,
代入点P(3,2)坐标可得$\frac{3}{a}$+$\frac{2}{a}$=1,解得a=5,
∴直线方程为x+y-5=0
综上可得所求直线方程为:2x-3y=0或x+y-5=0;
(2)当直线斜率不存在时,方程为x=1,与直线l:2x+y-6=0相交于B(1,4),
由距离公式可得|AB|=5,符合题意;
当直线有斜率时,设直线方程为y+1=k(x-1),
联立方程组可得$\left\{\begin{array}{l}{y+1=k(x-1)}\\{2x+y-6=0}\end{array}\right.$,解得B($\frac{k+7}{k+2}$,$\frac{4k-2}{k+2}$),
由距离公式可得($\frac{k+7}{k+2}$-1)2+($\frac{4k-2}{k+2}$+1)2=25,解得k=-$\frac{3}{4}$,
∴所求直线的方程为y=-$\frac{3}{4}$x-$\frac{1}{4}$,即3x+4y+1=0
综上可得所求直线方程为:x=1或3x+4y+1=0
点评 本题考查直线的一般式方程的求解,涉及截距式和分类讨论的思想,属中档题.

练习册系列答案
相关题目
3.若变量x,y满足约束条件:$\left\{{\begin{array}{l}{0≤x≤7}\\{2≤y≤8}\\{3x-y≥1}\end{array}}\right.$,则变量z=x-y的取值情况是( )
| A. | 既没有最大值也没有最小值 | B. | 有最大值5,没有最小值 | ||
| C. | 有最小值-1,没有最大值 | D. | 有最小值-5,也有最大值5 |
20.已知x1,x2分别是函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+2bx+c的两个极值点,且x1∈(0,1)x2∈(1,2),则$\frac{b-2}{a-1}$的取值范围为( )
| A. | (1,4) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | ($\frac{1}{4}$,1) |
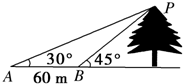 如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.
如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.