题目内容
已知两点M(-2,0),N(2,0),动点P在y轴上的射影为为H,|(Ⅰ)求动点P的轨迹方程,并指出方程所表示的曲线;
(Ⅱ)若以点M,N为焦点的双曲线C过直线x+y=1上的点Q,求实轴最长的双曲线C的方程.
解:(1)设动点的坐标为P(x,y),则H(0,y),
![]() =(-x,0),
=(-x,0),![]() =(-2-x,-y),
=(-2-x,-y),![]() =(2-x,-y).
=(2-x,-y).
∴![]() ·
·![]() =(-2-x,-y)·(2-x,-y)=x2-4+y2,|
=(-2-x,-y)·(2-x,-y)=x2-4+y2,|![]() |=|x|
|=|x|
由题意得|![]() |2=2
|2=2![]() ·
·![]() ,即x2=2(x2-4+y2)
,即x2=2(x2-4+y2)
即![]() =1(x≠0)
=1(x≠0)
(Ⅱ)由已知求得N(2,0)关于直线x+y=1的对称点
E(1,-1),则|QK|=|QN|
双曲线C的实轴长2a=||QM|-|QN||=||QM|-|QE||≤|ME|=![]() (当且仅当Q、E、M共线时取“=”),此时,实轴长2a最大为
(当且仅当Q、E、M共线时取“=”),此时,实轴长2a最大为![]() 所以,双曲线C的实半轴长a=
所以,双曲线C的实半轴长a=![]()
又∵c=![]() |NM|=2,∴b2=c2-a2=
|NM|=2,∴b2=c2-a2=![]()
∴双曲线C的方程为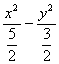 =1
=1

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 ,则点P的轨迹方程为
,则点P的轨迹方程为 