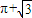题目内容
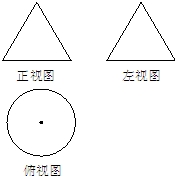如图，一个空几何体的正视图（或称主视图）与侧视图（或称左视图）为全等的等边三角形，俯视图为一个半径为1的圆，那么这个几何体的全面积为（ ）| A、π | ||
| B、3π | ||
| C、2π | ||
D、π+
|
分析：先管仔细观察给出几何体的主视图和侧视图便可知该几何体为圆锥，根据圆锥表面积公式的求法便可求出该几何体的全面积．
解答：解：仔细观察几何体的主视图侧视图可知该几何体为圆锥，
由图象可知：圆锥的圆心角为60°，圆锥的母线L长为2，半径为1．
根据圆锥表面积公式的求法：S=πRL+πRR=π×1×2+π×1×1=3π，
故选B．
由图象可知：圆锥的圆心角为60°，圆锥的母线L长为2，半径为1．
根据圆锥表面积公式的求法：S=πRL+πRR=π×1×2+π×1×1=3π，
故选B．
点评：本题考查了学生根据主视图、侧视图来判断几何体的形状以及圆锥表面积的求法，考查了同学们的观察能力和计算能力，属于基础题．
练习册系列答案
优化作业上海科技文献出版社系列答案
相关题目
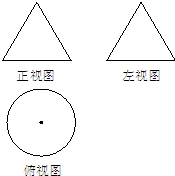
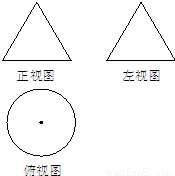如图，一个空几何体的正视图（或称主视图）与侧视图（或称左视图）为全等的等边三角形，俯视图为一个半径为1的圆，那么这个几何体的全面积为（ ）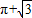
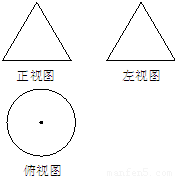如图，一个空几何体的正视图（或称主视图）与侧视图（或称左视图）为全等的等边三角形，俯视图为一个半径为1的圆，那么这个几何体的全面积为（ ）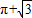
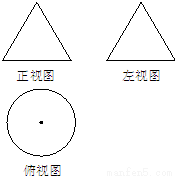如图，一个空几何体的正视图（或称主视图）与侧视图（或称左视图）为全等的等边三角形，俯视图为一个半径为1的圆，那么这个几何体的全面积为（ ）