Question

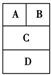
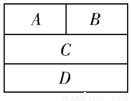
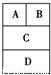
用4种不同的颜色涂入如图四个小矩形中，要求相邻矩形的涂色不得相同，则不同的涂色方法种数是（ ）

A．36
B．72
C．24
D．54

Answer 1

【答案】分析：本题是一个分步计数问题，把所给的四个矩形编号，首先涂1有C₄¹=4种涂法，则涂2有C₃¹=3种涂法，3与A1，2相邻，则3有C₂¹=2种涂法，4只与3相邻，则4有C₃¹=3种涂法．
解答：解：根据题意本题是一个分步计数问题，把所给的四个矩形编号
首先涂1有C₄¹=4种涂法，则涂2有C₃¹=3种涂法，
3与A1，2相邻，则3有C₂¹=2种涂法，
4只与3相邻，则4有C₃¹=3种涂法．
所以根据分步计数原理知共有4×3×2×3=72种涂法，
故选B．
点评：本题考查计数原理的应用，本题解题的关键是分析题目时时要按一定顺序，由相邻情况来确定可以涂色的情况数目，最后根据分步计数原理得到结果．