题目内容
已知函数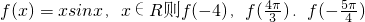 的大小关系为________.
的大小关系为________.
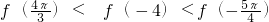
分析:判断函数f(x)=xsinx是偶函数,推出
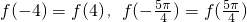 ,利用导数说明函数在(π,
,利用导数说明函数在(π, )时,得y′>0,函数是增函数,利用诱导公式转化从而判断三者的大小.
)时,得y′>0,函数是增函数,利用诱导公式转化从而判断三者的大小.解答:f(-x)=-xsin(-x)=xsinx=f(x)
f(x)为偶函数,所以比较f(-4),f(
 ),f(-
),f(- )的大小即是比较f(4),f(
)的大小即是比较f(4),f( ),f(
),f( )的大小;
)的大小;f′(x)=sin(x)+xcos(x)在(π,
 )内有f′(x)<0,所以f(x)在(π,
)内有f′(x)<0,所以f(x)在(π, )内递减,因为
)内递减,因为 <4<
<4< 所以
所以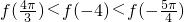 ;
;故答案为:
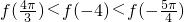 .
.点评:本题是中档题,考查正弦函数的单调性,奇偶性,导数的应用,考查计算能力,导数大于0,函数是增函数,是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 的大小关系为 .
的大小关系为 .