题目内容
函数 的图像与直线
的图像与直线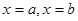 及
及 轴所围成图形的面积称为函数
轴所围成图形的面积称为函数 在
在 上的面积,已知函数
上的面积,已知函数 在
在 上的面积为
上的面积为 ,则函数
,则函数 在
在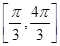 上的面积为 .
上的面积为 .
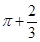
解析试题分析:求面积,要想办法利用已结论.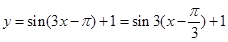 ,令
,令
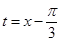 ,则上述问题转化为函数
,则上述问题转化为函数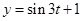 在
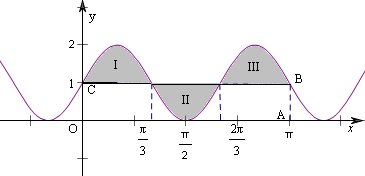
在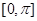 上的面积,作出
上的面积,作出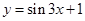 在
在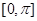 上的图象,如图,根据正弦函数图象的对称性,可把区域Ⅲ切下放到区域Ⅱ的位置,所求面积为区域Ⅰ的面积与矩形
上的图象,如图,根据正弦函数图象的对称性,可把区域Ⅲ切下放到区域Ⅱ的位置,所求面积为区域Ⅰ的面积与矩形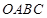 面积之和,
面积之和,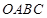 面积为
面积为 ,区域Ⅰ的面积等于函数
,区域Ⅰ的面积等于函数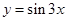 在
在 上的面积为
上的面积为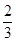 ,故所求面积
,故所求面积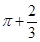 .
.
考点:三角函数图象的对称性.

练习册系列答案
相关题目
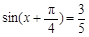 ,
,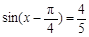 ,则
,则 = .
= . 为第二象限角,
为第二象限角, ,则
,则 ____________.
____________. 是第二象限的角,且
是第二象限的角,且 ,则
,则 的值为 .
的值为 . ,则
,则 .
. ,且
,且 ,
, ,则
,则 的值为
的值为 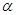 =2,求
=2,求 = .
= . ,
, ,则
,则 的值为________.
的值为________. 的图象为C:
的图象为C: 对称; ②函数
对称; ②函数 在区间
在区间 内是增函数;
内是增函数; 的图象向右平移
的图象向右平移 个单位长度可以得到图象C;
个单位长度可以得到图象C;