题目内容
已知函数f(x)= (a、b、c∈N),f(2)=2,f(3)<3且f(x)的图像按向量e=(-1,0)平移后得到的图像关于原点对称.
(a、b、c∈N),f(2)=2,f(3)<3且f(x)的图像按向量e=(-1,0)平移后得到的图像关于原点对称.
(Ⅰ)求a、b、c的值;
(Ⅱ)设0<|x|<1,0<|t|≤1,求证:|t+x|+|t-x|<|f(tx+1)|;
(Ⅲ)设x是正实数,求证: -f(
-f( +1)≥
+1)≥ -2.
-2.
答案:
解析:
解析:
|
解:(Ⅰ)函数f(x)的图像按e=(-1,0)平移后得到的图像所对应的函数式为 f(x+1)= ∵函数f(x)的图像平移后得到的图像关于原点对称. ∴f(-x+1)=-f(x+1),即 ∵a∈N,∴ 又∵f(2)=2,∴ 又f(3)= 由①,②及a,b∈N,得a=1,b=1 (Ⅱ)∵|f(tx+1)|=|tx+ 当且仅当|tx|=1时,上式取等号. 但0<|x|<1,0<|t|≤1, ∴|tx|≠1,|f(tx+1)|>2 S= 当|t|≥|x|时,S=4 当|t|<|x|时,S=4 ∴|t+x|+|t-x|≤2<|f(tx+1),即|t+x|+|t-x|<|f(tx+1) (Ⅲ)n=1时,结论显然成立. 当n≥2时, |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


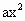 +1>0,∴-bx+c=-bx-c,∴c=0
+1>0,∴-bx+c=-bx-c,∴c=0 =2,∴a+1=2b,∴a=2b-1 ①
=2,∴a+1=2b,∴a=2b-1 ① <3,∴4a+1<6b ②
<3,∴4a+1<6b ② |=|tx|+|
|=|tx|+|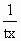 |≥2
|≥2 =2,
=2,
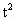 ≤4;
≤4;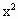 <4.
<4.
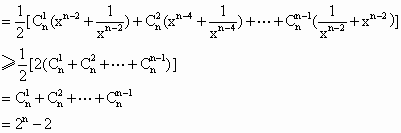
 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有